18世纪，牛顿和莱布尼兹的微积分被广泛地应用来解决前代人感兴趣的问题，如面积问题、极大极小值问题及描述悬挂着的链子的形状（即悬链线）或者振动着的弦上的点的位置问题；还有对于天体力学的应用，以及与函数性质有关的研究，所有这些领域还有其他领域在整个 18世纪发展了起来。这要归功于于泰勒、约翰·伯努利和丹尼尔·伯努利、欧拉、达朗贝尔、拉格朗日等人。

这些人使用了许多大师般的论证，但是这些论证的有效性又多有可疑之处。对这些大师来说，对发散级数的运算、虚数的应用以及对实无穷的运算，用得是得之于心、应之于手。然而这些方法，对于普通人，又总是很难解释清楚，所以有些结果再重复起来就不太可靠了。要做欧拉的计算，你就得自己就是欧拉，这种情况延续到了下一个世纪。

一些特定的争论突出了一些问题，而今天看来这些问题是来自基础上的混淆不清。例如，在无穷级数问题上，就有着形式表达式的适用范围上的混淆。考虑级数

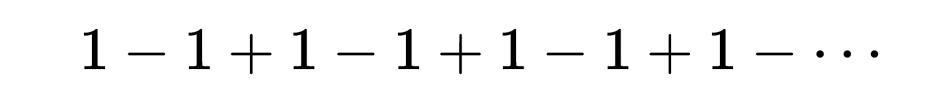
按照今天通用的初等定义，将把这个级数考虑为发散级数，因为它的部分和序列1，0，1，0……不趋向任何极限，但是关于这个式子却有争论。例如欧拉和伯努利就讨论过，一个无穷和的和与值可能有区别，伯努利认为，像1-2＋6-24＋120＋…这样的东西并没有和，但是这个代数表达式可以有值。欧拉则为下面的观念辩护说，级数的和就是产生这个级数的有限表达式的值，也不管这些名词究竟是什么意思。在他的1755年的一本书里，以

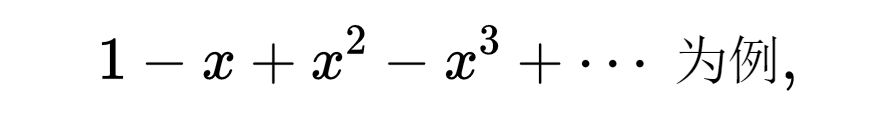
这个式子是由1/（1＋x）得来的，所以后来欧拉在为自己的观点辩护时，就说1-1＋1＋……=1/2。他的观点并未得到普遍接受。在把函数的值推到其通常的区域以外时，例如对于负数的对数，也产生过类似的争论。

对于18世纪的分析的语言和方法的最著名的批评家大概就是哲学家贝克莱。他的名言“存在即被感知”表明了他的唯心主义立场。他认为，这些对象应该是被感知的东西，而且应该是作为一个整体而被感知的。感知无穷小的大小的物体的不可能性，再加上它的明显的抽象性，使得贝克莱在他1734年出版的著作《分析学家：或致一位不信神的数学家的信》里讥讽地称无穷小为“消逝的量的鬼魂”，他的辩词是：在数学论证里、忽略去一个量，不论它多么小，都是不合适的。他引用了牛顿关于这个问题的话："在数学中，哪怕是最小的误差，也是不许可的。"贝克莱接下去又说，正是这门学科的晦涩使得牛顿把这类推理强加于他的追随者。

所有这些都表明，微积分需更深入的解释。

欧拉

欧拉对于分析的一般发展所作的贡献多于18世纪的任何人，他为了论证他的方法所给出的论据，由于他所写的重要的教科书的成功与被广泛采用，甚至在他身后仍然有极大的影响。欧拉的推理有时被认为是很不严谨，因为用起微积分记号来很是随心所欲，他的许多论证按后来的标准看也都是有缺陷的。特别当这些论证涉及无穷级数和无穷乘积时更是如此。一个典型的例子是他对以下式子的早期的证明：

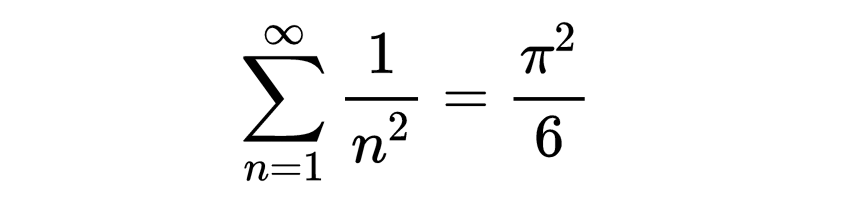
他的方法是这样的，利用sinx的已知级数展开式

欧拉考虑左式的零点，其位置在

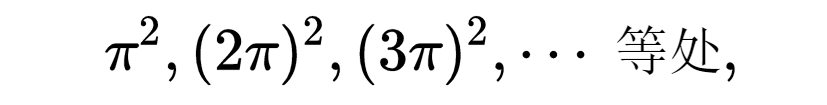
应用适用于有限代数方程的因式定理（而对此未作任何论证），他把这个式子写成

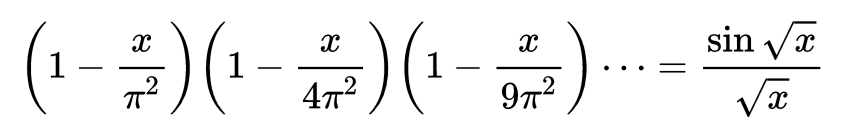
现在可以看到，双方x的系数应该相等。右式的系数是-1/6，而欧拉把左方各个括号都乘开，其中除了一个括号外都取1，这一项则取

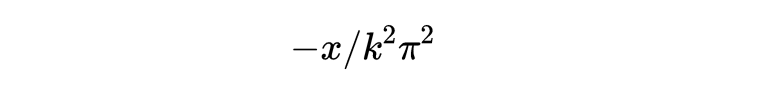
这样欧拉得到

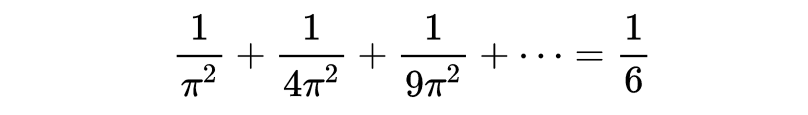
双方乘以π^2即得所求证明的式子。

我们现在认为这个处理途径有几个问题。无穷多个因子的乘积可能表示一个有限值，也可能不表示，今天就会要求确定它何时才表示一个有限值。还有把适用于（有限）多项式的结果用于无穷级数，是需要论证的步骤。欧拉在他的晚年对此结果给出另一个论证。他可能已经知道有反例一说。但是，这样的事实，对于欧拉却不是决定性的障碍。这样的观点，即在一般能行而可能有少数例外的情况下，仍然进行推理，在欧拉的时代并不少见，直到19世纪末，人们才通过协调的努力做到了这样的地步 ，即达到了这样的共识：在宣布分析的结果时，要确切地阐明这个定理成立的条件。

欧拉并没有细想过如何解释无穷和以及无穷小。有时，他轻率地就把无穷小当作零，而且从问题的上下文来导出微分之比的意义：

一个无穷小的量无非就是一个正在消逝的量，所以，将会真正变成零……所以在这个概念后面，和通常的想法不一样，并没有什么神秘的东西。这种假设的神秘使得无穷小的计算对于许多人变得很为可疑。

这个声明见于欧拉1755年写的Institutiones Calculi Differentialis一书，紧接着他就来讨论在比例中有一个比为0/0的问题，这样来论证在普通的数的计算中微分可以略去。这个声明很准确地描述了欧拉的实践的很大一部分——例如他在研究微分方程时就是这样做的。

然而，确实发生了冲突的事，而关于定义的辩论也不少见。最著名的例子涉及关于所谓振动弦问题的讨论。欧拉、达朗贝尔和丹尼尔·伯努利都卷进来了。这些辩论紧密地关乎函数的定义，以及在分析中所研究的函数有哪些可以用级数（特别是三角级数）来表示的问题。一条形状任意的曲线都可用作振动弦的初始位置，这样的思想推广了函数的思想，而傅里叶在19世纪早期的工作又使得这些函数在解析上可以处理。在这样的背景下，具有折断的图像的函数（一类不连续函数）就被纳入人们的视线了。后来，当与代数和三角运算相联系的"更自然"的对象让位于更一般的现代的函数概念时，如何对待这类函数，成了分析基础的决定性的问题。

18世纪晚期

在英国，对于贝克莱的一个值得注意的反应来自麦克劳林，他在1742年写的教本《论流数》试图澄清微积分的基础，消除掉无穷小量。麦克劳林是18世纪中叶所谓苏格兰启蒙时期的领导人物之一，是当时最出色的英国数学家，是牛顿的方法的热忱拥护者。他的著作，在欧洲大陆，和当时许多英国同时代人的著作不一样，得到了人们的阅读和兴趣、特别是他对牛顿天体力学的详细解释。麦克劳林企图用所谓"可指定的"有限量的极限这一概念作为他的推理的基础。麦克劳林的著作虽然确实给出了计算比的极限的例子，却是以晦涩著称的。他对于澄清分析基础的最大的贡献可能在于他对达朗贝尔的影响。

达朗贝尔读过贝克莱和麦克劳林的著作，而在拒绝无穷小量这一点上追随他们二人。当他探讨微分作为极限这个思想时，也企图把自己的思想与无穷小量可以无矛盾地看作是真正的零的思想调和起来、说不定这是对欧拉的思想的一种首肯。关于达朗贝尔的观点的主要作品可以在他主编的《百科全书》中关于微分的文章和关于极限的文章中找到。达朗贝尔为几何极限辩护，认为它比代数极限更重要。他的意思似乎是，对于所研究的量，不能仅仅作形式的研究，就是不能仅仅用代换和简化来研究。极限可以说是长度（或许多长度）的极限、面积的极限，或者其他有维度的量的极限，正好像把圆看成内接多边形的极限那样。他的目的似乎主要在于确立由现存的算法来描述的对象的现实性，因为他实际运用的计算是用微分来进行的。

拉格朗日

在整个18世纪里，微分学和积分学逐渐从它们对力学和物理学的应用中独立出来，成为一整套方法。同时，这些方法的焦点也从几何学移开，所以在18世纪后半叶我们越来越多地看到，微积分被处理为"解析函数"的"代数分析"。"解析"这个词在多种意义下使用。对于许多作者，例如欧拉，解析只不过就是讲的函数（作为变量之间的关系），即用分析中常用的单个表达式来表示的函数。

拉格朗日依据这种代数的观点为微积分提供了一个基础。拉格朗日集中注意于幂级数展开式，把它作为分析的基本实体，通过他的工作，解析函数这个词向着它的比较现代的意义演化，即与收敛的泰勒级数展开式相联系。他的途径在他1797 年的《解析函数论》一书里得到充分的表现。拉格朗日假设一个函数一定能表示为代数函数的无穷级数，他的这个论证是以已知的函数展开式的存在为基础的。他先是努力来证明在这个表达式里，"一般说来"不会有负幂和分数幂出现，由此他就得到了一个幂级数表达式。

这里的有点奇怪的记号是以拉格朗日的记号为基础的。设想要找出函数

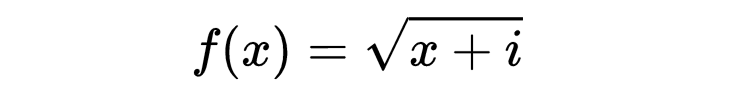
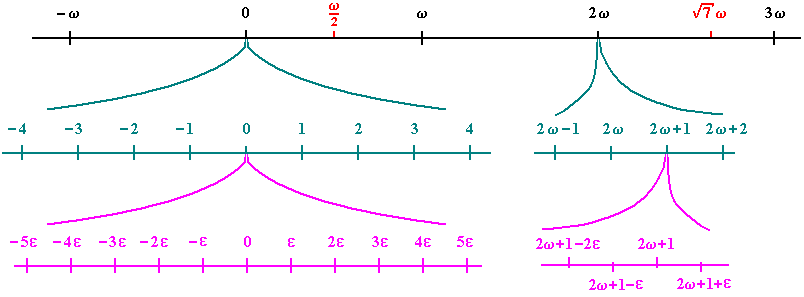
用i的幂的表达式。一般说来这里只会出现i的整数幂，因为，拉格朗日说，i^（m/n）这种形式的项是没有意义的，函数√x+i的表达式只有两个值，而i^（m/n）有n个值，而级数

可以从√x得到两个值，因此其他的项必定是i的正整数幂。把分数幂撇开以后，拉格朗日就论证说

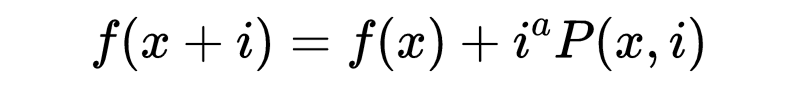
其中的P当i=0时是有限的。继续应用这个结果得到以下的表达式：

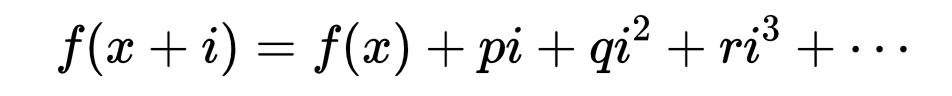
这里i是一个小的增量。数p也依赖于x，所以拉格朗日就定义它为f（x）的导函数，记作 p（x）=f'（x）。按照拉格朗日的用语，f（x）就是导函数的"原函数"。 类似的论据可以把高次的系数与通常的泰勒级数中的高阶导数联系起来。

以今天的眼光看来，拉格朗日的途径奇怪地有点循环论证的味儿，这是因为在18世纪把级数的“代数”无限过程与使用微分是区别开来的。拉格朗日并没有看到，原来的级数展开式就是以极限过程为基础的。由于重新强调极限，以及由柯西发展起来的新定义，拉格朗日的这个途径很快就被看成是站不住脚的了。