傅里叶与蒙日的伟大数学发现，成就了人类文明的一大部分

蒙日发明了画法几何（不要与射影几何相混淆）；傅里叶对热传导理论的经典性研究，开创了数理物理学的现代阶段。没有蒙日的几何学，19世纪机器的大规模生产也许是不可能的。画法几何是使机械工程成为现实的一切机械制图和图解方法的根源。由傅里叶在他关于热传导的工作中开创的方法，在边值问题中具有同等的重要性。因此，我们文明的相当大一部分，要归功于蒙日和傅里叶两人：蒙日在实用和工业方面，傅里叶在纯科学方面。

蒙日

加斯帕尔·蒙日1746年5月10日出生在法国的博纳。14岁的时候，蒙日在设计一辆消防车中显示出他各方面的特殊才能。他是一个天生的几何学家和工程师，有着使复杂的空间关系形象化的天赋。

在16岁时，蒙日因画了一幅出色的博纳地图而得到了物理学教授的任命。后来，蒙日也因此被送到军事学校去学习。在军事学校，他热衷于测量和制图的工作，这为他留下了大量的时间来研究数学，并成功地解决了一个重要的问题。

这就是画法几何的开始。蒙日把这个新方法教给未来的军事工程师们。以前像噩梦一样讨厌的问题，现在变得非常简单了。蒙日把画法几何当作一个军事秘密达15年之久。直到1794年，他才得到允许，可以在巴黎的师范学校公开讲授这种方法。拉格朗日听了一次演讲后说：“在听蒙日的演讲以前，我是不知道画法几何的。”

画法几何（或称作透视几何）是一种用于绘画和描绘三维空间物体的技巧和理论。画法几何的基本原理是通过模拟真实世界中物体在人眼中的视觉效果，将三维物体以二维的形式呈现出来。这种技巧可以帮助画家在绘画中创造出更加真实和逼真的画面效果。

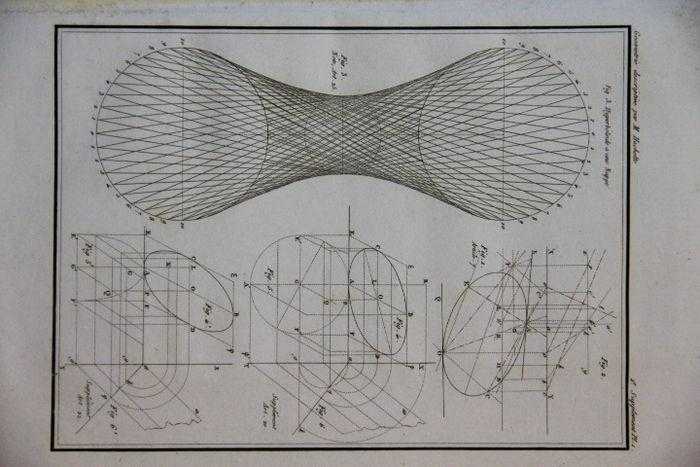
空间的立体或其他图形现在由两个投影描画在同一个平面上。例如，一个平面是由它的交线表示的；一个立体，比如说一个立方体，是由它的各条边和顶点的投影表示的。曲面与垂直平面和水平平面相交出曲线；这些曲线，或该曲面的交线，在一个平面上表示该曲面。

这样，我们就有了一种画法，它把我们通常在三维空间中看到的东西画在一张铺平的纸上。正是这个简单的发明革新了军事工程学和机械设计。它最明显的特点是简单明了。这个学科现在已经建立得很完整，以致专业数学家们对它已没有什么兴趣了。

此外，蒙日的名字与曲面几何联系在一起，这是微积分学中的重要内容。蒙日系统地用微积分学研究曲面曲率。在他的曲率的一般理论中，蒙日为高斯铺平了道路，高斯又启发了黎曼，而黎曼发展了在黎曼几何，并最终为相对论的建立提供了理论支撑。

1796年拿破仑的一封信开始了与蒙日长期亲密的关系。拿破仑非常欣赏蒙日的谈吐和无穷无尽的有趣见闻，蒙日则从这位总司令亲切的幽默中得到乐趣。当时在拿破仑身边的，还有傅里叶。

傅里叶

让·巴蒂斯特·约瑟夫·傅里叶1768年3 月21日生于法国的欧塞尔。他在13岁时是一个问题儿童，性格倔强，脾气暴躁。然后，当他第一次与数学接触时，他像着了魔似的，一下子转变了。为了学习数学，他去厨房里收集蜡烛头，他秘密的书房是在一张屏风后面的火炉边。

1789年12月，傅里叶（时年21岁）前往巴黎，把他关于数值方程解的研究论文送交科学院。这项工作超过了拉格朗日，至今仍然很有价值。但是由于傅里叶在数理物理学方面的方法已超过了它，我们就不再进一步讨论它了。

拿破仑看出了无知的士兵们将成事不足败事有余。为此，拿破仑于1794年创办了高等师范学校。傅里叶被聘为数学教授。这项任命，开创了法国数学教学的新纪元。这个计划的成功超过了人们的预期，并且导致了法国数学和科学史上最光辉的时期之一的来临。在综合工科学校，他以罕见的引证历史的方法，使数学课活跃了起来，他还巧妙地用一些有趣的实际应用，来说明抽象的问题。

傅里叶的《热的解析理论》是数理物理学的一个里程碑。他在1807年提交了第一篇关于热传导的论文。拉普拉斯、拉格朗日和勒让德是评阅人。他们在承认傅里叶的工作的创新性和重要性的同时，指出其在数学处理上还有缺点，在严格性方面还有许多有待改进之处。拉格朗日本人曾经发现过傅里叶主要定理的一些特殊情形，但他没能得到一般结果。

顺便提一下，纯数学家和数理物理学家之间的一个基本区别。纯数学家所能用的唯一武器是精确、严格的证明。除非所引证的定理能够经得起它的时代所能提出的最严格的批评，否则纯数学家们几乎是不会用到它的。另一方面，应用数学家和数理物理学家们会设想无限复杂的物质世界能用简单到人类能够理解的任何数学理论完全地描述。

科学家们为了科学本身而对数学采取的这种冷淡态度，激怒了一类纯数学家，就像遗漏一个可疑的小小的下标而激怒了另一类迂腐的学究一样。结果是只有很少几个纯数学家对科学作出过重要贡献。开尔文勋爵无视傅里叶关于热学分析的杰作中明显缺乏严格性，而称它为"一首伟大的数学诗"。

正如已经说过的，傅里叶的主要研究方向，是边值问题——微分方程的解适合指定的初始条件，这也许是数理物理学的中心问题。自从傅里叶把这个方法应用到热传导的数学理论中来，极有天赋的人们已经比他曾经梦想过的走得更远了，但是他那一步是决定性的。在他做的事情中，有一两件非常简单，可以在这里加以叙述。

在代数中，我们要需要画出简单的代数方程的图形。但是反过来，什么样的方程会导致像下图中的这种无限重复的线段的图形呢？

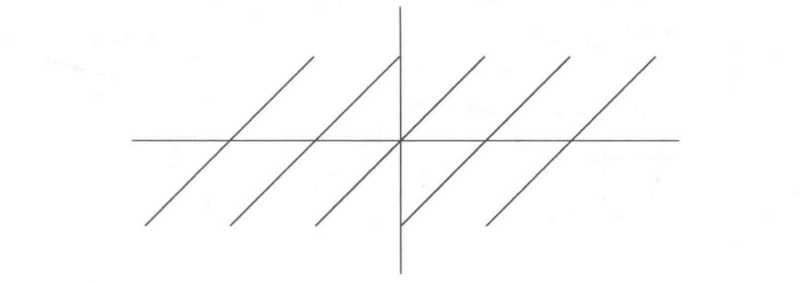
这样的由不相连的直线段或曲线段构成的图形，在物理学，例如热学、声学和流体运动的理论中反复出现。可以证明，不可能用有限的、精确的数学表达式把它们表示出来。但“傅里叶定理”提供了一种从数学上表达和研究这种图形的方法：在某个区间内连续，或者在该区间内只有有限数目的不连续点，且在该区间内只有有限数目的转向点的给定的函数，可表示成正弦或余弦函数的无穷和，或正弦和余弦函数两者的无穷和。

既然提到了正弦和余弦，我们就回想一下它们最重要的性质，即周期性。设下图中圆的半径是1个单位长度，通过圆心0画互成直角的轴，如在笛卡儿几何中那样，标出AB等于2π单位长度；这样，AB在长度上等于圆的周长。

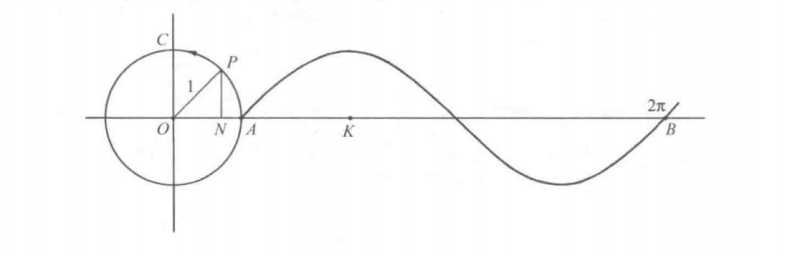
设点P从A开始，沿箭头所示的方向描出圆的轨迹。画PN垂直于OA。那么，对于任何位置的P，NP的长度称为角AOP 的正弦，ON称为角AOP的余弦；NP和ON像在笛卡儿几何中那样取它们的符号（NP在OA上方取正号，在OA下方取负号；ON在OC的右边是正的，在OC左边是负的）。

不论P在任何位置，角AOP是4个直角（360°）的一部分，相应于弧AP 在整个圆周上所占的部分。所以我们可以沿着AB标出弧AP在2π中所占的相应比例，以表示这些角AOP。这样，当P在C处时，经过了整个圆周的1/4；因此，相应于角AOC，我们在距离A点长度为1/4AB处有点K。

在AB上的每一个点，我们画长度等于相应角度正弦的垂直线段，根据正弦是正或负，决定垂直线段在AB的上方或下方。这些垂直线段的不在AB上的那一端落在图中所示的连续曲线，即正弦曲线上。当P回到A 点，开始重新沿着圆转时，曲线在B以后重复，如此以至无穷。如果P向相反方向旋转，曲线就向左重复。曲线在一个2π区间后重复：角（这里是AOP）的正弦是一个周期函数，周期是2π。

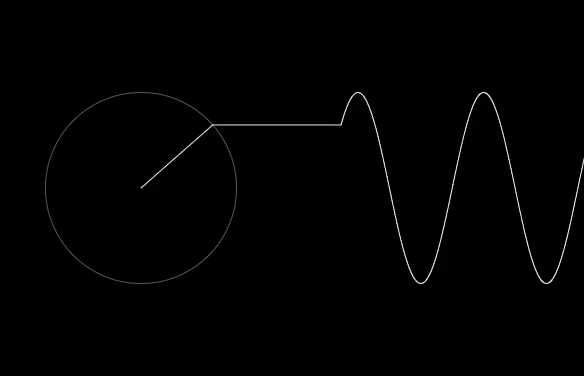
不难发现，sin2x通过一个完整周期比sinx快一倍，因此它的一个完整周期的图形是sinx的一半那么长。同样，sin3x的完整的周期是2π/3等等。这对于cosx，cos2x，cos3x，…也同样成立。

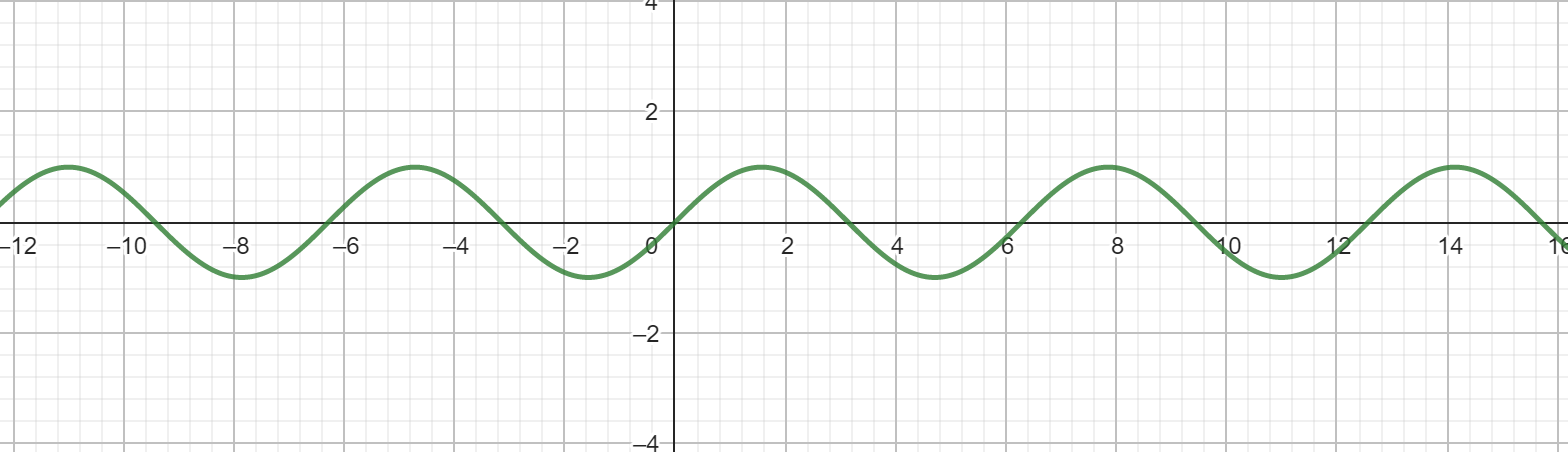
现在能够大致描述傅里叶的主要数学成果了。在已经提到的与“间断"的图形有关的限制内，任何具有明确确定的某个图形的函数，都能用下面这种类型的方程表示：

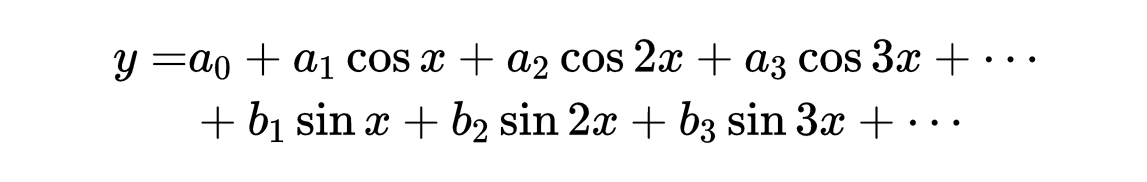
其中省略号表示两个系列按照某种规则无限地继续下去，当任何x的已知函数y是已知时，系数

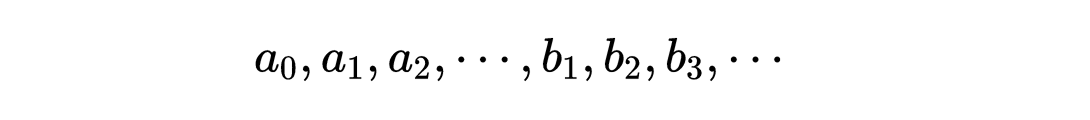
是可以确定的。换言之，任何x的已知函数，比如说f（x），能够展开成上述类型的级数，即三角级数或傅里叶级数。所有这些都只在某些限制条件下才成立，这些限制幸而在数理物理学中不很重要；例外的情形是一些很少有或没有物理意义的的情形。再重申一次，傅里叶级数这项工作是边值问题的第一个伟大的成就。

上面所描述的周期的概念，对于自然现象具有明显的重要性，潮汐、月相、季节以及人们熟知的许多其他事情，本质上都是周期性的。有时候一个周期现象，诸如太阳黑子的反复出现，能够用一定数目的简单周期性图形相叠加而很好地逼近。因此这些现象就能化简为一些独立的、简单的周期现象，而原来的周期现象是由它们组合而成的。

在现实世界中，很多自然现象都具有周期性，例如：

天文现象：月相、日食、年季节等都具有周期性，这些现象可以用周期函数进行描述和预测。机械振动：振动是指物体在固定点周围作周期性的往复运动。机械振动的研究可以帮助人们了解机械设备的运动规律和稳定性，以及如何调节和控制机械振动。电信号：电信号在传输过程中也具有周期性，例如交流电和数字信号等。周期性的特点使得信号可以在传输过程中被分割成不同的时间段进行传输，从而提高了信号的传输效率。生物节律：人体内的许多生理现象，例如心跳、呼吸、睡眠等都具有周期性。了解这些生物节律的规律可以帮助人们更好地维护健康。

当他在1822年完成1807年开始的工作，并收集在关于热传导的专著中时，人们发现固执的傅里叶对他原先提交的论文一个字也没有改动。1830年5月16日，他因心脏病去世，享年63岁。