数学和理论物理这两个领域只属于少数天才，所以大众整不明白也并不奇怪。能整明白，就可以以此为职业了。高维空间的数学研究很早就开始了，但在物理学使用这些概念前，研究这些概念的数学家大多被大众当成无害的怪人，整天想些虚幻不实的东西。

图示：数学是物理学的基础，而且通常数学家的想象力总是走在物理学需要的前面，因此在数学和物理学界有个古老的玩笑，上帝一定是个数学家。

直到物理学发展到需要借用高维空间几何分析，来解决物理学上遇到的实际问题的时候，这些概念才开始慢慢进入大众视野，也开始吸引到大众对高维空间的兴趣。为什么物理学家需要用更多维度来解释宇宙呢？

因为，三维空间无法容纳解释宇宙奥秘的大统一方程！

物理学家相信整个宇宙的基础——注意是基础——都可以用一个“简单"的方程加以描述，这被称为物理学的万物理论，也被称为终极理论。在研究终极理论的过程中，物理学家们发现只有三个维度的空间无法解决这个问题，必须要扩张空间的维度才行，而让他们感到惊喜的是，早在物理学提出自己的需要之前，已经有数学家们在百年前就开始了探索高维空间中的几何问题的研究可以拿到物理学中用。

图示：如果存在宏观高维，万有引力也将在这个维度上施展它的影响，这将严重影响我们已知的世界

至于宇宙在微观尺度上到底多少维，这个问题并没有定论，当然这里的所有额外的空间维度，都蜷缩在极小的空间中，存在于量子世界中，宏观世界只有三维这一点毫无疑问，否则万有引力都要出问题。太阳系中的行星都将无法维持现有轨道。

我们这代人难以想象高维空间，但有了现代计算机的帮助下，我们的后代将不会再像我们这一代这样对高维几何茫然不知，或许以后的高考中，就会有高维几何数学考试题，到那一天就不会有人问这种问题了。

图示：用计算机做出的四维超立方体三维投影动画，可以帮助我们理解它，并想象第四个垂直方向。

"平凡"的高维：一分钟顿悟高维空间

在日常生活中，更高维度属于科幻小说范畴。但在数学世界里，高维并不是什么特别的东西。虽然我们很难直观想象它们，我们生活的世界，每个点只需要由三个坐标定义，因为无法想象另一个进入方向，因此我们难以想象四维物体。

但如果用代数而不是几何，制造高维物体就并不困难。

首先来看一个单位圆，即半径为1，圆心位于原点（0,0)的圆，它的代数表示形式为：

x²+y²=1

上面这个方程定义了圆环上每个点的位置，即不多也不少，当你把这个代数方程转变为几何图形时，你就会得到一个单位圆。

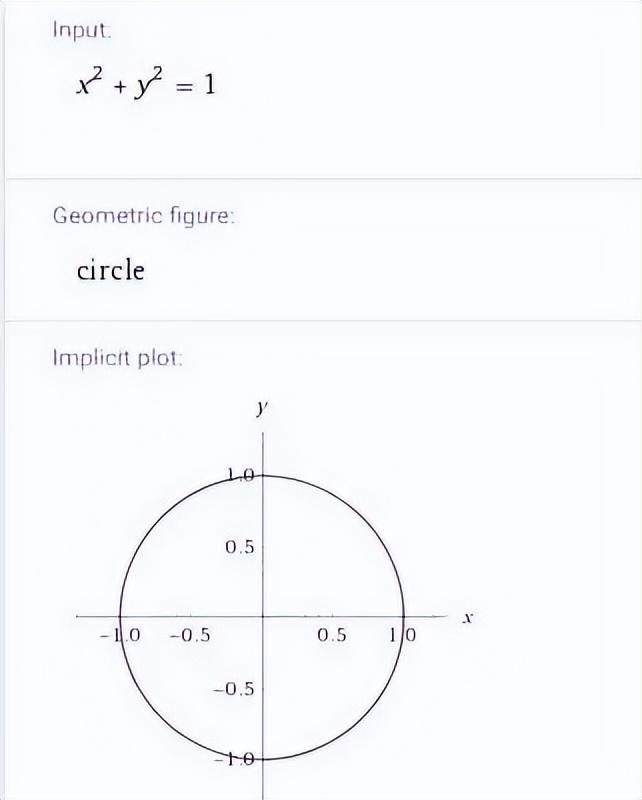
图示：标准单位圆 via wolframalpha

现在，让我们在维度上跨出第一步，从二维进入我们同样熟悉的三维空间，要如何改造我们的代数方程：

x²+y²=1

以便用它来表示一个三维的单位圆球的球面上每一个点所在的位置呢？三维单位圆球，就是球心在三维原点（0,0,0)，并且球的半径为1的球。

非常简单！

x²+y²+z²=1

增加一个变量z即可，不信，那让我们用计算机把这个方程式的几何图形画出来看一眼吧。

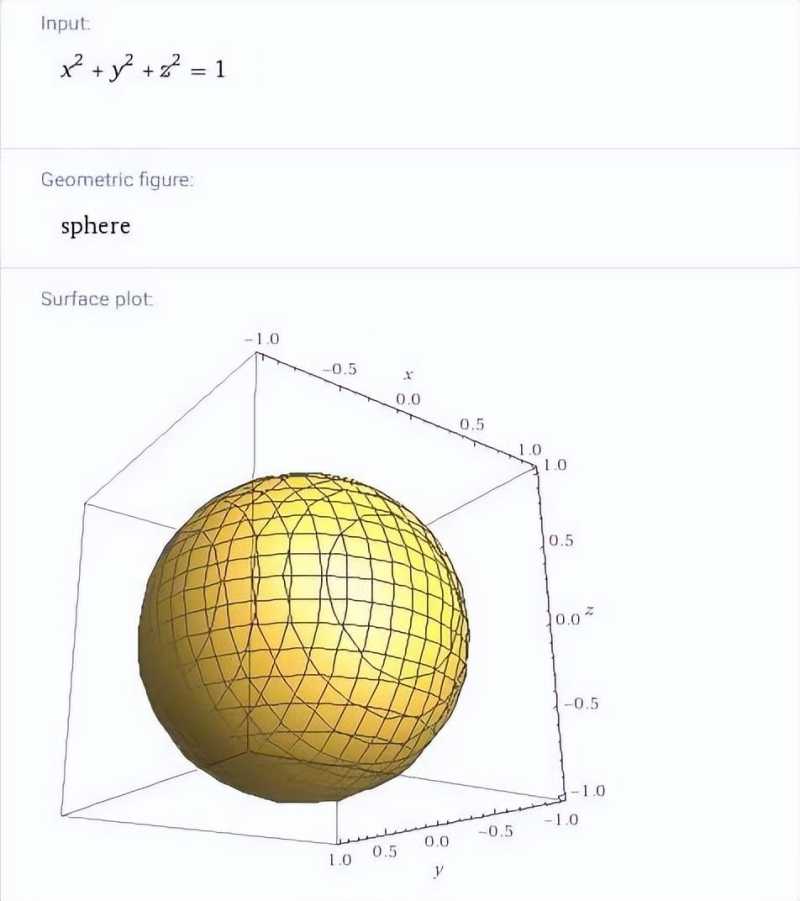
图示：看到了吗，这是一个三维圆球，球面上的每个点距离圆心的距离都是1

现在，让我们继续。

如果我们这样写方程式，

x²+y²+z²+s²=1

增加一个神秘变量s，这在几何学上意味着什么呢？

它意味着我们写出的是一个四维空间的单位超球体上的每一个球体距离超球体球心（0,0,0,0)的距离都是1。我们可以用文字进行叙述，但我们已经无法画出也无法想象这东西了。当然我们可以通过降维的方法画出它的三维投影。

图示：它拒绝画图了，因为这是一个四维超球体

注意维度是这么增加的。

圆的环——在二维平面中存在的一维闭合曲线

圆球的球面——存在于三维空间中的二维闭合曲面

超球体的球体——存在于四维空间中的超球面

我们还可以继续增加变量，依次得到五维、六维乃至N维空间中的超超超超

...

超球。

所以在几何上难以想象的高维物体，在代数上可能并没有那么难。

当然，我们只讨论了最简单的球体，而其它形状的几何体，是否存在相应的高维空间版本，这个问题必须具体问题具体分析。但

但上述例子也是希望大伙儿了解一下，用代数研究高维物体也有很简单的时候，并非全都难得超越普通人能掌握和理解的范畴。

我们是怎么知道，自己生活在三维空间的？

最早认识到空间是有维度的观念，至少可以追溯到亚里士多德，他在其著作《天空》中表达过这样的观念：线在某种程度上非常重要，因为它定义了平面，也定义了实体，从长度到面积，从面积到体积。

天文学家托勒密则将这一基本观念进行了量化，他可能是第一个明确提出三维空间的人，托勒密为此专门写了一本讨论空间维度的书《维度》，在这本书中托勒密完成了一个重要证明，那就是证明我们所生活的空间维度不多不少恰好是三维。自此三维空间在西方知识阶层中慢慢成为必须知道的常识。

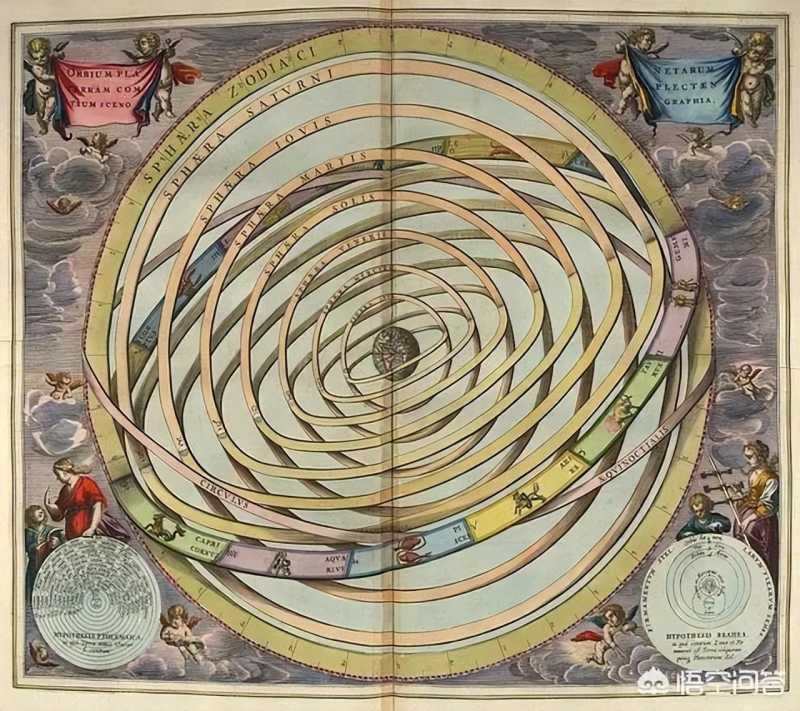
图示：托勒密构造的和谐宇宙天球系统，在这个系统中，地球是宇宙的中心，所有其它天体都围绕地球运动，而空间到底有几个维度，就是个很重要的问题，搞不清这件事，是无法规划整个天球体系的。

公元二世纪中期，托勒密在其发表的《维度》一书中这样写道：

距离是天体之间非常重要的一个属性，要试图理解宇宙的奥秘，我们首先必须对距离进行定义。

但我们要如何定义距离呢，当我们对距离进行测量时，怎样的测量才是合理的测量呢？

托勒密明确提出一个重要原则：垂直关系，他说，我认为定义距离必须沿垂直线进行

如果是这样，那我们可以发现空间中的任何一个点，都可以被三条彼此垂直的线锁定，这三条彼此垂直的线，两条用来定义平面，第三条则测量纵深，除此之外再找不出第四条垂直线。这就是为什么说我们生活在三维空间中的根本原因 。

图示：三维空间本质，从原点到空间中的任意一个点

如果两点间不存在一条直接简单连接的直线时，我们只需要三个彼此垂直的线段，就总是能精确到达三维空间中的任意一个点，不需要第四个垂直线段，也不存在第四个垂直线段，这就是三维空间的本意了。

超越三维？

数百年前的数学家大多认为任何超越三维的物体都是怪物，是纯粹的空想，毫无意义。

最先明确提到超越三维空间实体的数学家是Stifel（施蒂费尔，1486-1567），他说：

超立方体仿佛像有三个以上的维度

但马上他就声明：这是反自然的

而数学家John Wallis（约翰·沃利斯）更加旗帜鲜明，他说：

任何高于三维的空间对象是怪物，甚至比奇美拉（Chimaera）或半人马（Centaure）都要怪异。长宽和高度，已经占据了整个空间。凡人无法想象在这三者之外，如何还能存在第四个空间维度。

但数学家奥扎拉姆（Ozanam，1640-1717）则玩了个小花招，他首先表示尊重传统，即任何高于三个维度的实体都不是真实的，但他同时也小心翼翼地指出，数学有能力处理超越三维的事物，他相信数学能找到一套自洽的处理高维实体的数学方法，甚至多到如字母表那样多的维度（字母表有26个字母）。

从考虑高维空间实体的角度，发明莫比乌斯环/带的数学家莫比乌斯，提供了第一个将三维实体转变成四维实体的例子，莫比乌斯环将由此变成著名的克莱因瓶。

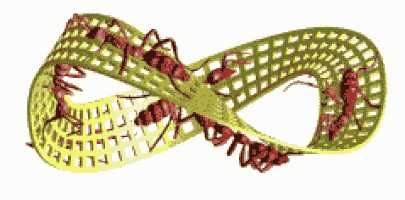
图示：嵌入三维空间中的二维莫比乌斯带，可以帮助我们理解高维空间。

通过将二维平面在三维空间中扭转后黏贴在一起可以实现让平面的两个面自然过渡的效果，即在从一个面爬往另一个面的时候，没有明显的翻越障碍的地方，不知不觉就到了另一个面，而且这个循环无休无止。想象一下，如果我们的宇宙也是一个嵌入到四维空间中的三维的实体，那么宇宙就可以即是有限的，同时又是没有边界的，你永远飞不到宇宙的边界，你只会回到原点。

将莫比乌斯带在四维空间中黏贴到一起，可以得到另一个知名四维空间物体——克莱因瓶。

图示：装不满的克莱因瓶

克莱因瓶被称为瓶，只是因为它在三维空间中的投影像一个瓶子。与莫比乌斯带相似，只是将维度提一等，莫比乌斯带对于二维生物来说是个让人迷惑的东西，那么克莱因瓶对于我们这样的三维生物来说也同样迷惑。因为这个瓶子没有内外之别，如果我们真的拥有一个真实的克莱因瓶，就会发现一件怪事，那就是这个看起来没有缝隙（在三维空间中没有）的瓶子，是永远也装不满的！因为任何装入瓶中的物体，仿佛突然间拥有了穿墙术，它们会通过神秘的第四维漏出来！

换句话说，要是有一个真实的克莱因瓶，人类就可以真正的研究第四维了！但这东西只能在四维空间中制造得出来，在三维空间中是无法制造的。就像上面那个莫比乌斯带，只能通过三维空间制造，无法在二维平面中造出来，虽然你可以把它投影到二维平面上，那就是一个扭转的8字。

虽然在合成几何学上要在想象中制造高维实体都很麻烦。

但对于分析几何来说，只要不把高维几何体变成需要人类去想象的实体，仅仅是在数学上处理它们，则并没有想象中那么困难。

1833年，数学家格林尝试探索高维空间几何的分析方法。

1847年，数学家柯西在《几何与分析》中宣布找到处理高维几何的数学方法

1854年，数学家黎曼提出 “关于几何基础的假设”，讨论了N维空间中的流形，黎曼正式引入了无界但有限空间的概念，这一突破与四维几何形状密切相关。而黎曼几何是爱因斯坦广义相对论的数学基础。

到19世纪末期，四维或更高维几何图形的专著和论文数量开始急剧增加。到1911年，Sommerville列出了1832篇研究高维空间的重要参考文献，它们用意大利语，德语，法语，英语和荷兰语写成。高维空间研究在数学界已经是一个重要研究分支。