数学公式之十大最美丽的数学方程式都有哪些,你认为谁应该是第一
我对一个漂亮的数学方程的主观定义基于两个主要因素:方程的简单性和我使用它时的满足感。我为这个列表所做的一些选择对新手数学家来说并不简单,但对经验丰富的数学家来说却非常简单。
我列表中的选择仅限于我所涵盖的 BSc/MSc 数学模块的知识。如果您觉得您有建议应该在此列表中,请随时发表评论。
谷歌对“等式”的定义将一种含义列为“将一件事等同于另一件事的过程”。
因此,如果一个方程式、定义或以其他方式带有“=”符号,那么我认为它有资格被列入我的列表,即使有些人可能会说它在数学上不是真正意义上的方程式。
10. x 的 x 次方导数
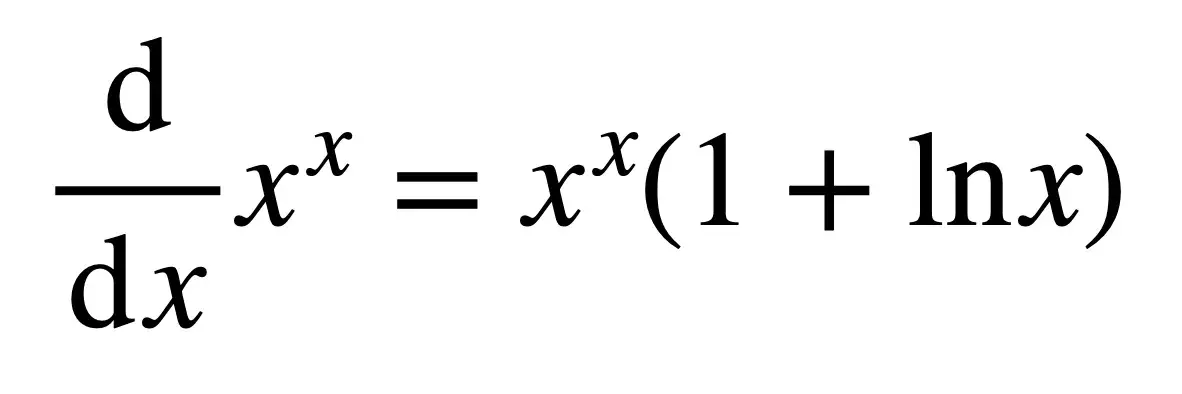
也许只有我一个人认为上面的方程很漂亮,但是一旦你理解了如何计算左边,它就会非常令人满意。
如果你已经学习了高级数学,那么你可能会认为这个导数相当可怕。
对我来说,解决这个导数感觉就像五星级的三道菜的数学等价物。
首先是对x、指数和自然对数之间美妙关系的认识。
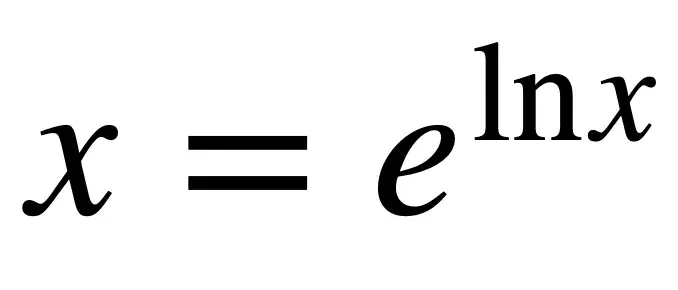
接下来,这个规则的应用。
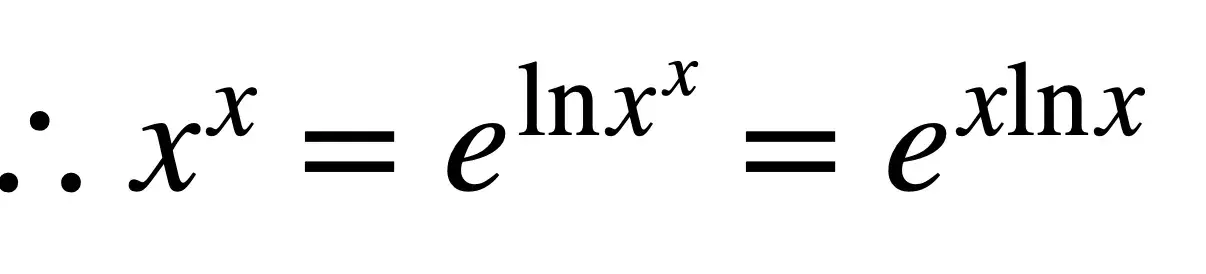
现在我们终于可以证明左边等于右边。
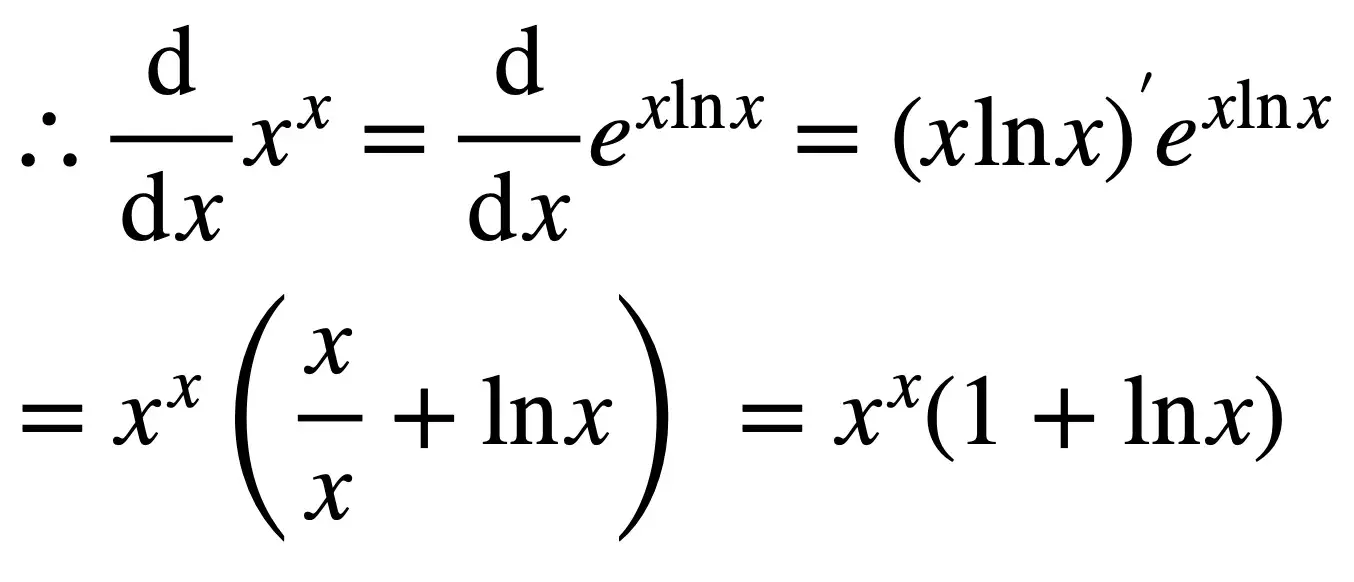
对我来说,这个问题展开的方式既美丽又有益。它以一种紧凑的方式结合了幂、指数、对数和微分规则。
9. 群的定义

群定义描述了一个集合“ E ”和一个运算符“star”来结合“E”的两个元素以产生一个“E”的元素,以遵守群公理(结合性、恒等式和逆元的存在)。
“星号”运算符可以表示任何运算符,例如乘法、加法、减法或除法——它基本上等同于“ x ”,但对于运算符而言。
我认为它很漂亮,因为它以符合简单的方式在视觉上代表了一个群体。
8. Aleph noel,自然数的个数
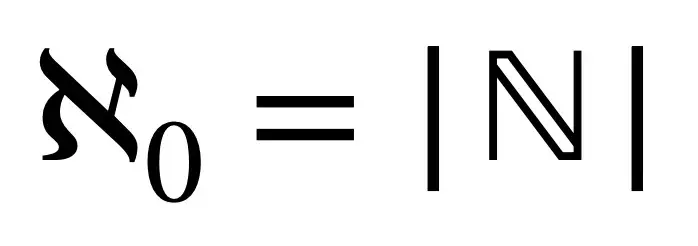
Aleph noel 被定义为自然数的个数(即正整数的个数)。换句话说,对于那些不熟悉自然数集的人来说,它是一组从 1 开始向上计数的整数正数(即 1、2、3、4、5 等),这就是为什么它们是称为“计数”:
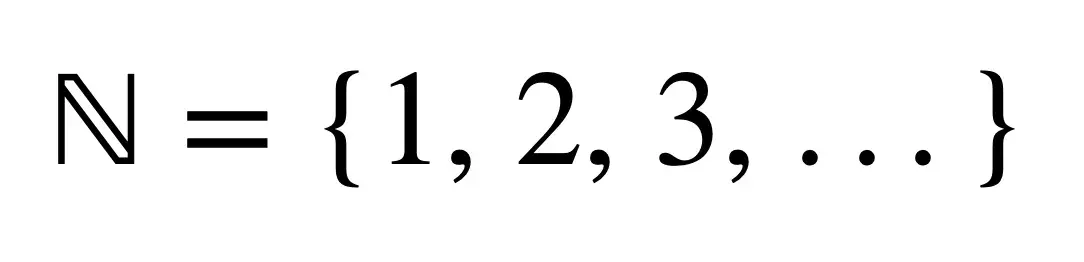
那么这个集合中有多少个数字呢?无穷?我们将其描述为 aleph noel 的无限量。可能很想说:
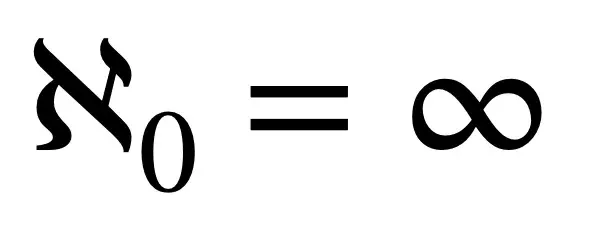
但这不是全部事实,因为有比 aleph-noel 更大的无限数量。例如,实数的个数(整数和小数的个数)也是无限的,但它包含的不仅仅是正整数的个数,所以它一定是比正整数的个数更大的无穷个数。所以当你听到数学家或物理学家说某些无穷大比其他无穷大时,这确实是数值现实。
7. P = NP(有争议)
P VS NP 问题是计算机科学和决策数学中最大的开放性问题。它提出了一个问题,即在多项式时间内被非确定性算法接受的每种语言是否也被多项式时间内的确定性算法所接受。
如果所有 NP 问题(在多项式非确定性时间内易于验证但难以求解)都在 P(在确定性时间内易于求解和验证),则 P = NP。
如果“P = NP”被数学界接受,在我看来,它会被证明是最美丽的方程之一。
6. 质能等价
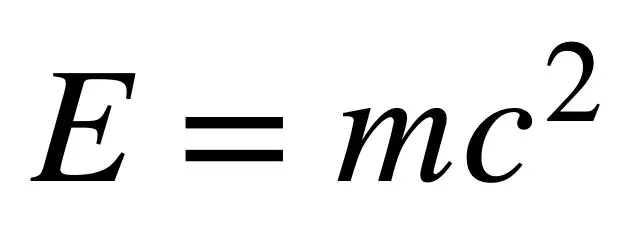
爱因斯坦著名的方程建立了质量、能量和光速c 之间的美妙关系。
5.牛顿第二定律
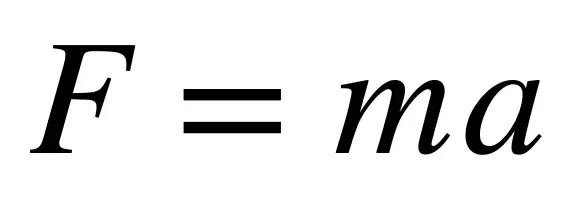
牛顿第二定律不仅简洁优美,而且从某种意义上说,它也是紧凑的,因为对于不同的场景,同一方程式有许多版本。这是一个方程式,需要时可以简单,需要时可以复杂。
我最喜欢的F = ma版本是 Navier-Stokes 方程,它本质上是F = ma的重写,用于通过将流体建模为连续体来描述流体的运动。我最喜欢的方程式版本如下:
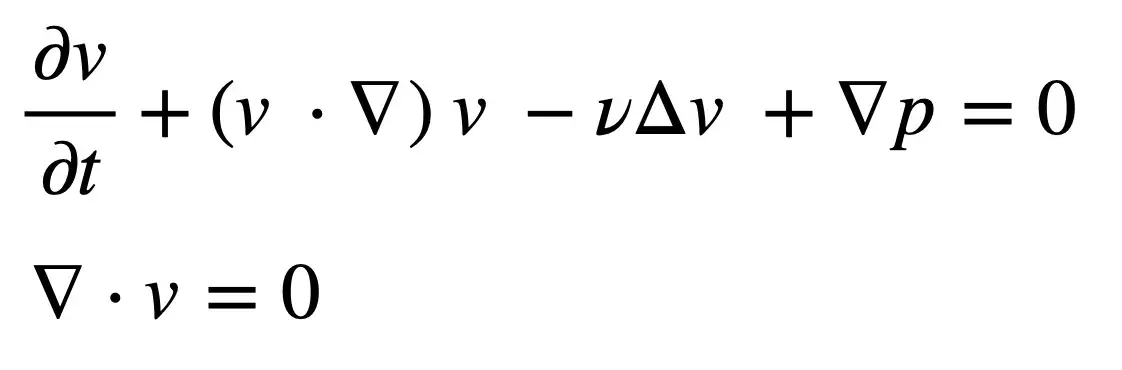
4.零阶乘
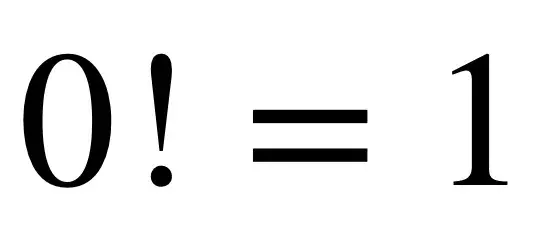
我发现这个等式很漂亮,因为它和谐地将 0 和 1 结合在一起,但又不使它们相等。
除了作为零阶乘的答案之外,这同样可以被程序员理解为“0 不等于 1”,这似乎是我过去试图将 1 除以零或计算倾向于计算极限的反复出现的主题在不首先解决分母的情况下为零。
3.欧拉恒等式
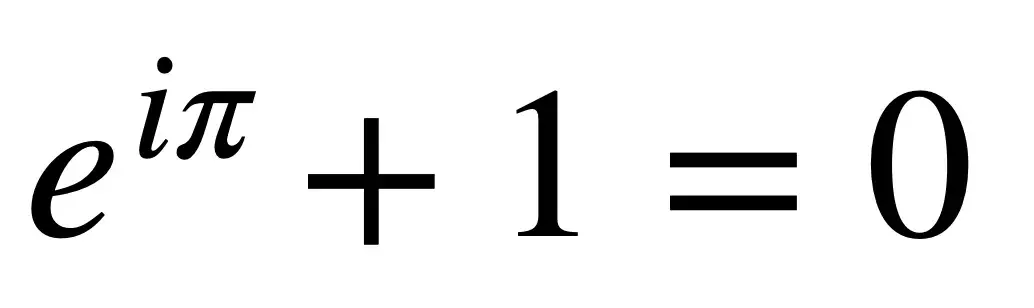
欧拉恒等式可以使用德莫伊弗定理求得。我们知道 cos(π) = -1 和 sin(π) = 0。根据毕达哥拉斯定理,我们还知道半径r为 1。因此,将这些值代入 De Moivre 定理,复项i sin(π) 消失,我们得到漂亮的欧拉恒等式 exp(iπ) = -1。这个方程式可以重新排列成上面的方程式,我认为它更漂亮,因为它包含了零。
它被数学界的许多人认为是一个非常漂亮的恒等式,因为它显示了 π, i和欧拉数e之间的显着联系。
2.一加一等于二
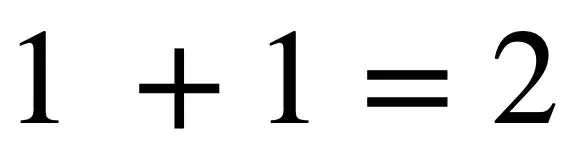
这可能看起来相当幼稚,但当我们考虑到数学在人类历史上取得了长足的进步时,即使是数学的基础也不能被视为理所当然。
它也是我生命中第一个将我引入数学领域的方程式。
1. -1的平方根
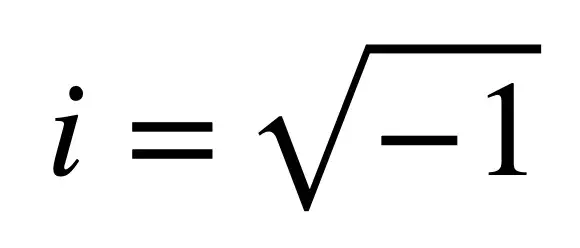
当我第一次在一本更深入的数学教科书中看到这个方程时,我被这个方程的纯粹美丽和简单所震撼。
复数的概念和学习它们在量子力学中的应用确实让我觉得自己仿佛进入了一个全新的数学世界。
我记得我在学校时想学习进阶数学的主要原因之一就是了解“虚数”是什么。当时它似乎非常有趣,现在复数感觉就像数学的任何其他重要方面一样。
总结
感谢您阅读我最喜欢的十大数学方程式列表。
大家都在看
-
世界上等级最高的体育赛事:奥运会每四年一届,已举办了29届 世界上有许多各式各样的体育赛事,吸引着全球范围内的观众们的目光。无论是足球、篮球、网球,还是自行车赛、电子竞技,都有自己的粉丝群和观众基础。但要说到世界上等级最高的体育赛事,非奥运会莫属,也是最具影响 ... 体育之最08-19
-
世界上等级最高的足球赛事,世界杯每四年一届 足球这项风靡全球的运动,拥有着无数狂热的粉丝。而在所有足球赛事中,世界杯无疑是最为耀眼的明珠。世界杯的起源可以追溯到1900年的法国。当时国际足球协会主席罗伯特·格林倡议并组织了第一届世界杯。起初世界杯并 ... 体育之最08-19
-
12岁于子迪200米蝶泳夺冠:泳坛新星的破晓之光 12岁的于子迪以一记酣畅淋漓的夺冠,在200米蝶泳赛道上划出了属于中国泳坛的璀璨弧线。这位少年泳将的横空出世,不仅让观众惊叹于其超越年龄的竞技实力,更点燃了人们对中国游泳未来的无限遐想。她的胜利,是天赋与 ... 体育之最05-23
-
专访邓亚萍:不服输的态度永不止步 “绽放”,一个富有生命力与美感的词汇,形容女性力量的苏醒与成长。在北京世界妇女大会三十周年、中国将再次召开全球妇女峰会之际,在全国妇联宣传部的指导下,新京报推出女性力量主题报道《绽放》,记录新时代中国 ... 体育之最05-23
-
42岁老将血战王曼昱!削球艺术对决,险胜背后是永不屈服体育精神 多哈世乒赛女单1/16决赛赛场见证了一场跨越年龄与伤病的经典对决——中国选手王曼昱苦战五局,以4-1险胜42岁的德国华裔老将韩莹。这场66分钟的鏖战不仅展现了顶尖的技战术博弈,更诠释了体育精神的真谛。首局开始, ... 体育之最05-23
-
21分钟速胜!孙颖莎碾压卢茨创纪录,外媒惊叹:中国女乒无解 在近期乒乓球赛事的舆论场中,运动员孙颖莎的赛场表现引发了全民热议。社交媒体平台上涌现的数十万条评论,既折射出公众对体育竞技的炽热关注,也投射出当代社会多元化的体育价值认知。通过梳理这些充满激情的民间表 ... 体育之最05-23
-
最佳运动时间不是“天刚亮”,更不是“临睡前”!很多人锻炼错了 你会选择早上锻炼还是晚上运动?近日一项最新研究发现最佳运动时间既不是“天刚亮”更不是“临睡前”!最佳运动时间不是“天刚亮”2023年,广州医科大学和广东省人民医院的研究人员在《自然·通讯》期刊上发表的研究 ... 体育之最05-22
-
冲上热搜!战胜国乒后激动捂脸痛哭,这才是竞技体育最真实的模样 大冷门!日本选手战胜国乒后激动捂脸痛哭:这一刻,他们等了多久?!乒乓球,作为中国的“国球”,是无数国人的骄傲。每一次大赛,国乒队员们的表现都牵动着亿万球迷的心。而对阵日本队,更是每次交锋都火花四溅、扣 ... 体育之最05-22
-
多哈乒坛风云:热血与遗憾交织的竞技诗篇 赛场如战场,胜负只在瞬息之间。2025年5月的多哈世乒赛,上演着无数令人心跳加速的瞬间,冷门与惊喜轮番登场,让全世界的球迷为之疯狂。黎明未至,球馆内已剑拔弩张。刚捧起世锦赛桂冠的日本名将平野美宇,本是夺冠 ... 体育之最05-21
-
CBA生死战启示录:当钢铁之躯轰然倒下,谁在改写英雄剧本? 当胡金秋在总决赛第六场首节轰然倒地的瞬间,超过百万直播观众的手机屏幕都闪过同样念头:"广厦完了"。这位场均25+12的常规赛MVP得主,在争抢篮板时被对手撞击腰部后蜷缩在地,伴随剧烈呕吐被搀离球场。但这 ... 体育之最05-21
相关文章
- 国际乒联的“傲慢”才是体育精神?
- NBA史上最强的10个最人都有那些!
- 为什么它能称为地球最受欢迎的运动?这些数据告诉你答案!
- 跳水台上的冰与火:00后双姝巅峰对决撕开竞技体育最残酷的温柔
- 国乒狂揽四连胜!孙颖莎碾压神秘之师,王曼昱双线突围引爆看点
- 最适合人们的体育运动,大多数人都不知道
- 勒布朗-詹姆斯最新推特:体育赛事中最棒的两个字—抢七!
- 伽VS普拉提:谁才是你的“本命运动”?90%的人都选错了!
- 34岁孙杨带伤夺铜!赛后一动作让全网泪崩:这才是真正的冠军
- 世乒赛首日惊爆冷门!国乒主力碾压韩国天才,朝鲜队成最大黑马
- 梁靖崑14-12绝境翻盘!三大战术撕碎神秘之师,国乒外战稳如磐石
- 跳水女皇陈若琳如若水,润泽时光的永恒水池之美
- 近20年中国最具影响力的10位体育运动员名单(第一集)
- 为什么说跳绳是“运动之王”?骨科医生说出几个好处,早了解
- 奥运体坛最漂亮的5位女运动员,身材好颜值高,你最喜欢哪位
- 伟大,格雷格·波波维奇打造体育史上最伟大的辉煌之一
- 攻克国内之最!黄河体育中心专业足球场成功“戴冠”
- 马龙职业生涯中的几个“之最”?
- 盘点那些足球之最,这些球星你认识几个?
- 2024年我国运动员获194个世界冠军创历年之最
热门阅读
-
NBA75大球星官方完整名单 02-15
-
世界十大顶级体育赛事:奥运会居第二,世界杯局魁首 08-23
-
2022热门网游排行榜前十,英雄联盟位居第一宝座 09-02
-
steam免费游戏排行榜前十名,不用花钱又好玩 09-03


















