美索不达米亚八边形的文化和数学意义：新视角下的伊斯兰艺术设计

女士们，先生们，老少爷们儿们！在下张大少。

伊斯兰艺术设计中最常见的正多边形是八边形。使用八边形和八重玫瑰花结的历史证据可以追溯到美索不达米亚的杰姆代特·奈斯尔(Jemdet Nasr)(公元前3100-2900年)。此外，在古埃及，八边形可以在数学问题(Ahmose纸莎草纸，编号48)，家庭用品(纸莎草纸存储)，建筑(花岗岩柱子)和装饰品(宫殿装饰品)中找到。正八边形是伊斯兰艺术设计的一个基本的重要元素，在米索不达米亚和其他正多边形一起被广泛用作算术对象。八点星形多边形长期以来一直是古代苏美尔女神伊南娜和她的东方闪米特对手伊师塔的象征。在新亚述时期，八重玫瑰花结偶尔取代星星作为伊师塔的象征。在本文中，我们讨论了八边形设计是如何从九世纪晚期开始在伊斯兰地区流行，并从Jemdet Nasr到公元前三世纪末一直存在于美索不达米亚。本文描述了正多边形的几何图案，包括正八边形，在伊斯兰世界发展的原因。此外还讨论了正多边形的数学意义。

介绍

在Pierre Paulin (1927-2009)的作品、巴黎歌剧院的天花板(19世纪)和塔什干UMS大厦的立面(图1)中都可以找到规则的八边形。在伊斯兰艺术中，这些图案分别被称为8重玫瑰形、8星多边形和8点星形(见图5)。

图1：(a)皮埃尔·波林的作品(b)巴黎歌剧院的天花板(c) UMS大楼

伊斯兰艺术设计可分为书法、多边形几何图案和阿拉伯图案。书法有两种类型：楷书(kufic script，见图2)和草书（cursive script）。

图2：“穆罕默德”的阿拉伯文，古尔埃米尔，撒马尔罕

多边形的几何图案可以被发现是抽象的优雅组合。在乌兹别克斯坦，优雅组合的例子很普遍。在Ulugh Beg madrassah (1417-1420)中使用常规的5、6、8和16边形，在Gur-i Emir (1403-1404)中使用常规的4、5和6边形(图3)。布哈拉的阿卜杜拉汗(1588-1590)的宗教学校的圆顶建筑使用规则的五边形、六边形和七边形(Makovicky，1986: 971)。我们还可以在塔什干的Kukledash宗教学校(十六世纪中期)找到规则的5边形、6边形和10边形的优雅组合(图4)。

图3：(a)乌鲁·拜格·马德拉萨(1417-1420年)(b)古尔·埃米尔(1403-1404年)

图4：塔什干Kukledash Madrassah

伊斯兰几何装饰的历史特点是从七世纪初到九世纪末，在九世纪末，几何图案在穆斯林建筑师和艺术家中盛行(Abdullahi和Embi, 2013: 242446)。几何在伊斯兰艺术设计中起着核心的重要作用。星形多边形是伊斯兰艺术设计中最重要的元素，其构造完全由圆圈决定。Critchlow(1999: 8)指出，圆是主要的宇宙学符号，是整体性和统一性的象征，Abdullahi和Embi(2013: 245)声称，圆是宗教的象征，强调一个神和麦加的滚动。

在这篇论文中，我们研究了自九世纪晚期以来盛行于伊斯兰地区的八角形设计是如何在美索不达米亚存在的，以及为什么包括正八边形在内的正多边形的几何图案在伊斯兰世界得到了发展。此外，我们还讨论了正多边形的数学意义。

八星形多边形和八重玫瑰花结的存在可以追溯到美索不达米亚的Jemdet Nasr时代(Wolkstein & Kramer，1983: 184，Friberg，2007a: 166)。此外，在古埃及，八边形包括伪八边形的使用可以在Ahmose纸莎草纸(问题编号48，公元前17世纪晚期)、家庭用品(纸莎草纸储存，大约公元前1400年)、建筑(花岗岩柱子)和装饰品(宫殿装饰品)中找到。

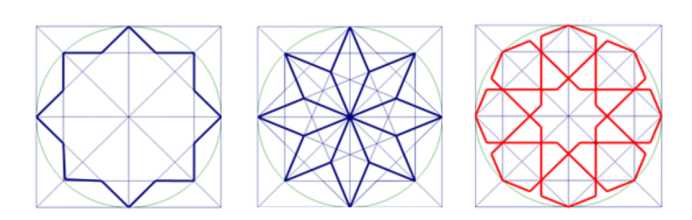
图5：(a) 8点星形，( b) 8点星形多边形，(c) 8重玫瑰形

正多边形是伊斯兰艺术设计中一个基本的重要元素，在美索不达米亚的度量代数中通常被用作算术对象。八点星或八重玫瑰一直是女神伊南娜/伊师塔的象征，即维纳斯。伊南娜的符号出现在Gawre时期(大约公元前3300年)的印章上(Wolkstein & Kramer，1983: 190)。正八边形被认为是在伊斯兰世界通过整合艺术、数学和宗教而发展起来的。这与Ettinghausen的主张一致，即由于缺乏自己的传统，蓬勃发展的伊斯兰文明不得不借鉴早期的传统(Lewis，2002: 72)。许多特征，如多边形设计，被认为是典型的伊斯兰教可以追溯到穆罕默德之前的时代。

正多边形、度量代数和点对称

在古巴比伦数学中，度量代数是一个恰当的术语，指的是结合了几何学、计量学、一次和二次方程的特殊类型的数学。从原始苏美尔人(公元前第四个千年的末期)到塞琉古时期(公元前第一个千年的末期)，度量代数已经广泛传播。规则的3、4、5、6、7和8边形是巴比伦度量代数中非常重要的对象。古巴比伦数学家擅长构建适当大小的正多边形和形式化表达式，例如:

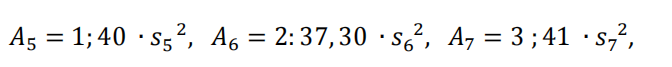
其中An表示面积，sn表示正n形的边长(Friberg，2007a: 161)。特别地，正六边形被用来求圆的周长(Neugebauer，1957: 47)。一块泥板上写着六边形的周长是0；57，36倍外接圆的周长。在这种情况下，π ≈ 31/8比3更接近π。

在度量代数中，两个给定的同心圆之间的古阿卡德方带是突出的(Friberg, 2007a: 77-8；胡贝尔，1955:106)。基于VAT 8521和Eshnunna文本IM 67118中度量代数问题求解算法的几何解释，Friberg提供了两种方法，如图6所示，从旧阿卡德方带中构造一个正方形(Friberg, 2007a: 78)。

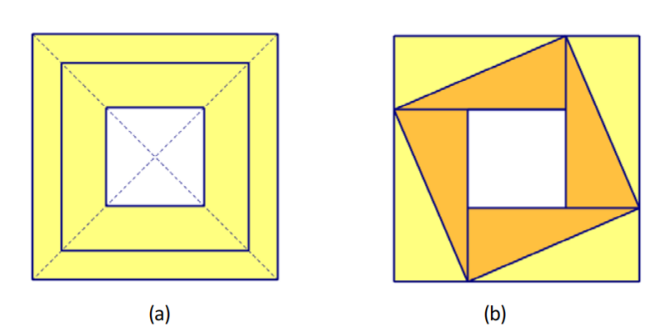
图6：古阿卡德方阵的两种构造方法

图7：塔什干，古阿卡德方阵和人行道街区中间的一种建造方法

巴比伦天文学家使用与图6(a)相关的方程来计算木星沿着其黄道60天路径运行一半的时间(Ossendrijver，2016: 484)。此外，Friberg基于IM 67118 (Friberg，2007b: 206)中求解过程的基本思想，提出图6(b)作为毕达哥拉斯定理的可能的古巴比伦证明。一些研究人员认为，古巴比伦的数学家为“直角三角形链”起了一个名字，就像图6(b)中显示的橙色直角三角形所形成的那样。这种直角三角形的点对称在外观上类似于楔形数字符号sar = 60 × 60(图8(b)) (Friberg，2007b: 206)。

正方形内的点对称图案是伊斯兰艺术中流行的图案(Critchlow, 1999: 72)。此外，这种点对称图案可以追溯到原始苏美尔人的Jemdet Nasr时期(见图8(a)) (Friberg, 2007a: 167)。特别地，我们将使用图6(b)来检查卡拉坎墓塔的砖砌几何图案。

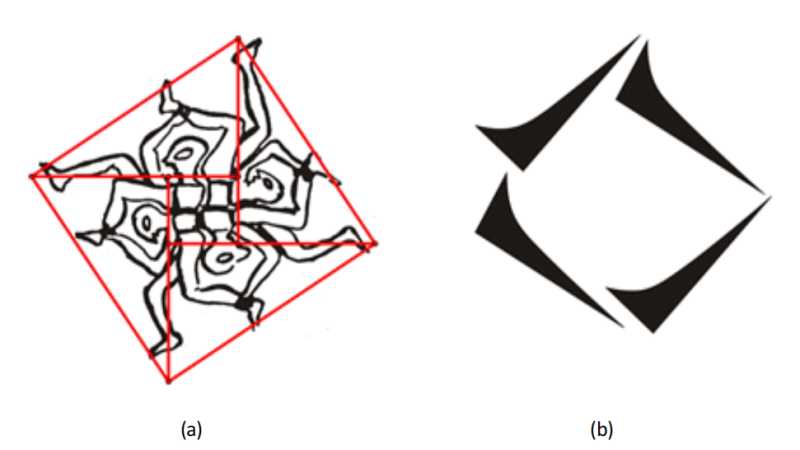
图8：点对称图形和sar符号

由于数字7不是费马素数，正七边形不能用圆规和直尺来构造(Dummit and Foots, 2004: 602)。古巴比伦人在度量代数中粗略地构造了正七边形。TMS 2(rev.)泥板部分丢失(见下图9)。然而，等腰三角形的高度被认为是有记录的(Friberg, 2007a: 162-163)。六边形周长的每条边的长度是30。可以推测，圆的周长约为7∙30 = 3 30，因此直径为110，半径为35。

图9：TMS 2(修订版)，卢浮宫博物馆

现在，让我们仔细看看TMS 2(rev .)中的构造过程(图9)。首先，古巴比伦人画了一个半径为35的圆，并用一条30的线或一根30的棒在粘土的每个角上显示一个小洞。古巴比伦人在用线段连接后抹去了圆。在图9的左上角有一个圆被擦掉的痕迹。在假定古巴比伦人熟悉八边形的情况下，Friberg建议根据其边对正八边形进行详细的度量分析(Friberg，2007a: 155-159)。

正八角形及其伊斯兰艺术设计

简单的六边形和八边形作为几何图案被用于伊本图伦清真寺(开罗，879)。抽象的六边形和八边形可以在哈拉坎(伊朗，1067年)的墓塔中观察到，也可以在Al-Juyushi(埃及，1085年)的清真寺中观察到(Abdullahi和Embi，2013:245；内西波卢，1995年：99)。

El-Said和Parman在Kharaqan的墓塔中发现了两个由八边形组成的图案(图10，如下)和四个由六边形组成的图案。此外，他们还分析了10至17世纪伊朗、摩洛哥、印度、土耳其、阿富汗、也门和伊拉克使用的几何图案(El-Said和Parman，1976：第二章)。

墓塔的抽象八角形图案(图10)被归类为壁纸群中的“ppm”(Martin，1982: 108)。

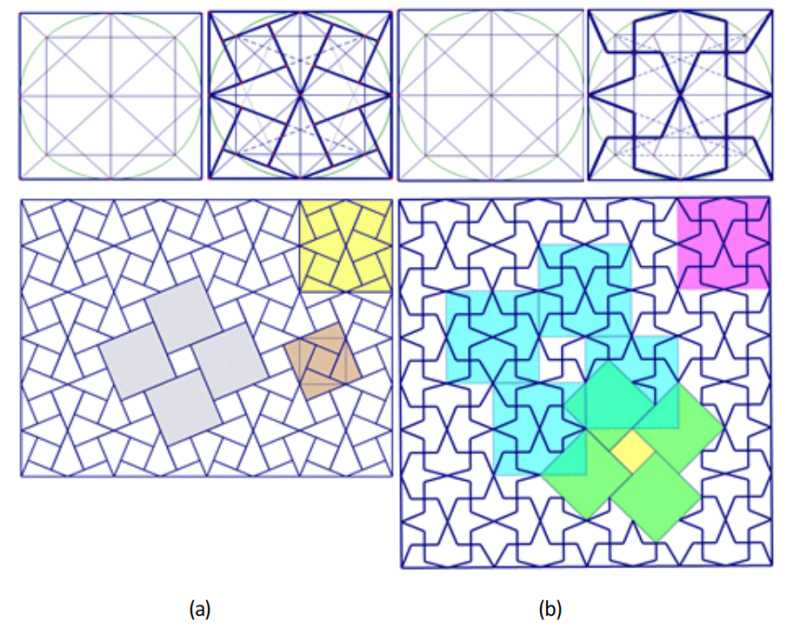
图10：卡兹文卡拉干墓塔八角形图案的几何分析

图10(a)和图10(b)包括墙纸组中被归类为“p4”的两个矩形图案。这样的设计在人行道上很常见。

图11：塔什干的两个矩形人行道街区

此外，图10(a)还包含一个由四个菱形(或旋转的风筝)组成的圆环(见图12)和八角形装饰(见图13)。

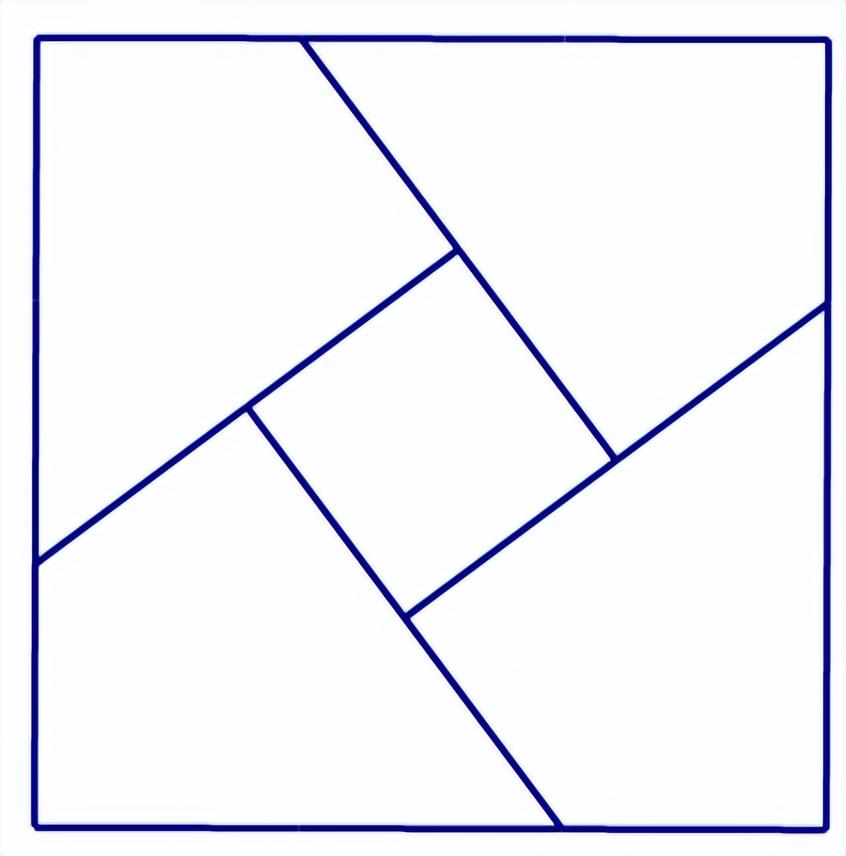
图12：由四个菱形组成的环

图13：塔什干Kharraqan墓塔及其人行道砖砌图案的八角形解释

Friberg (2007b: 206)提出了IM 87118的几何解释，该解释涉及在给定面积和对角线的情况下确定矩形的边长，如图6(b)所示。此外，他还更新了hy RUP和Damerow的列表，其中直接或间接使用了对角线规则(Friberg，2007b: 450)。

我们提出了一种可能性，即四个菱形的环设计(图12)源自中途的旧巴比伦方块(图14(b)，如下)，与对角法则的证明有关，通过颠倒位于每个角的四个直角三角形(图14(b)，如下的着色部分)(Park & Kim，2017: 45)。因此，我们称之为四菱形(或风筝)的环改变旧阿卡德方带。这个名字反映了古代阿卡德人的数学(VAT 8521)和古代巴比伦人的数学(IM 87118)。

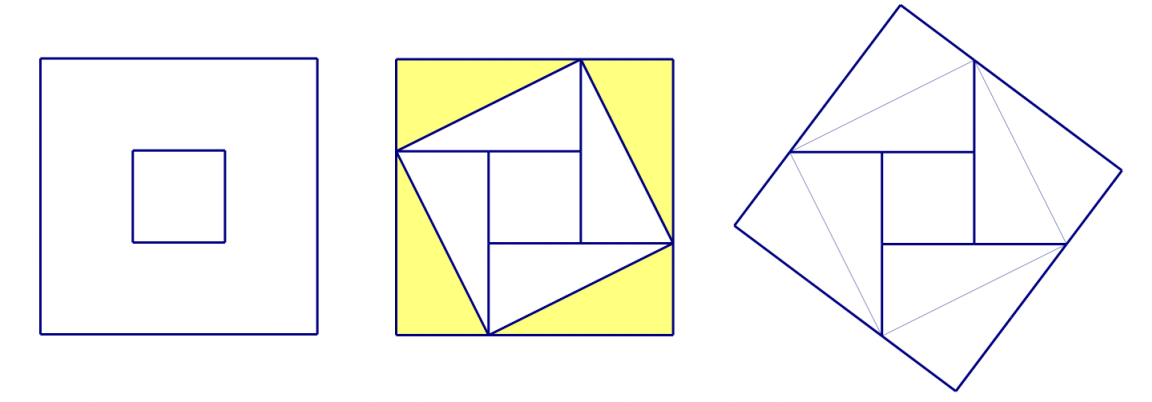
图14：(a)旧阿卡德方带，(b)中间方带，(c)改变后的方带(图纸:J. Park)

图15：Khiva的木门，四个矩形的圆环

图16：撒马尔罕Tillya Kari Madrassah (1646-1660年)中四个菱形环的几何解释

Chorbachi (1989: 761-763)通过视觉描述和对基本几何结构的连续描绘，解释了哈拉真砖砌图案中的旋转设计。另一方面，克伦威尔和贝特拉米(2011: 86)声称四菱形环在(图17)方面受到了中国人的影响。赵爽对《周髀算经》(中国，公元前250年)的注释包含了支持勾股定理的论据和图表。但是，原始图表丢失了。图17显示了被认为是“赵爽的斜边图”(Katz，2009；204-5).

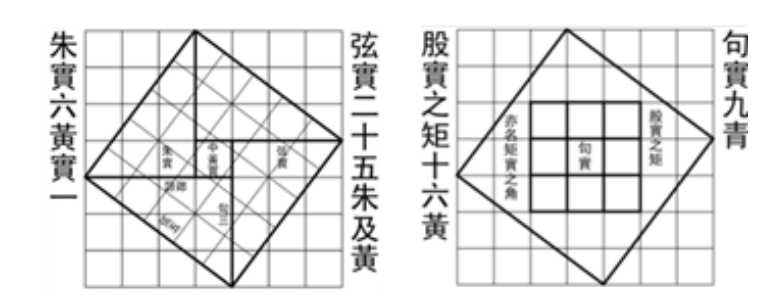
图17：赵爽的斜边图的估算图

根据弗里伯格基于对IM 87118的几何解释的学说，可以合理地假设旋转风筝是受古巴比伦的影响，而不是受中国的影响。

正八边形的起源

在本节中，我们将研究在Jemdet Nasr、阿卡德王朝、古巴比伦、新亚述和新巴比伦时期存在的8星多边形。

图18：哈拉夫文化陶瓷碗，卢浮宫

图18描绘了在美索不达米亚北部的Arpatchiyah发现的哈拉夫文化(公元前6000-5100年)彩绘陶瓷碗的重建碎片(卢浮宫博物馆指南)。它似乎反映了植物叶子的形状，因此很难将该设计视为八边形几何形状的几何表达。

正八边形与对角线的几何识别可以从乌尔古城著名的皇家墓地下面挖掘的粘土印章印中看到(Friberg, 2007a: 166)(见下图19)。勒格兰声称制作日期为Jemdet Nasr(公元前3100-2900年)(弗里伯格，2007a: 164)。8星多边形可以在游戏板上找到，被称为二十格游戏，来自乌尔早期王朝皇家墓地(Robson, 2008: 46)。此外，在Jemdet Nasr时期的圆柱体印章中也存在两个8星多边形，这是女神伊南娜的星符号(Wolkstein & Kramer, 1983: 184)。

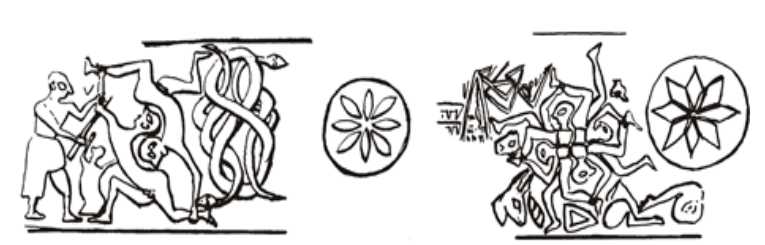
图19：(a) UE 3，286 (b) UE 3，393(图纸:J. Park)

考虑到每个菱形都是椭圆形的，可以合理地将图19(a)视为8重玫瑰花结的第一个例子之一。所述椭圆形状可由花瓣形状或谷地形状衍生而来。巴比伦人区分了薄椭圆形和厚椭圆形，分别称为麦田和牛眼(图20中的AEBO ')，如TMS 3所示(Friberg, 2005: 134;2007: 323 - 4)。前者用圆弧内嵌正方形构造，后者用圆弧内嵌等边三角形构造(见图20)。这些也是度量代数的主题。

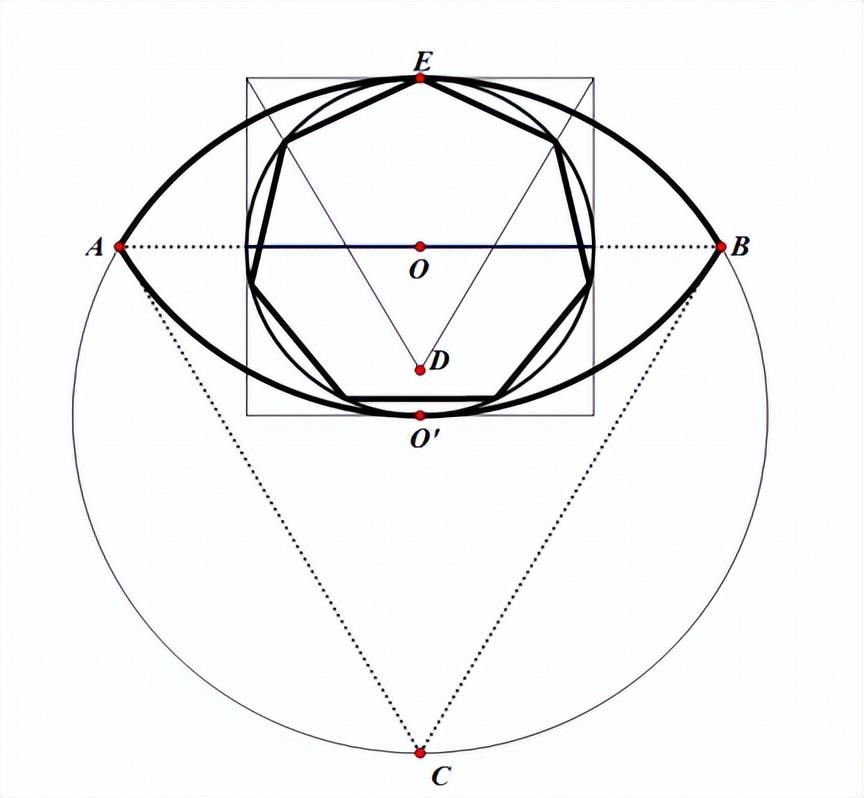
图20：带有牛眼的七边形结构

古巴比伦数学家确定短轴(EO′)和长轴(AB)的长度，用√2 ≈ 17/12表示粮田，用√3 ≈ 7/4表示牛眼(Friberg，2005: 134，135)。牛眼在几何学中的作用似乎非常重要。牛眼确定给定线段的垂直平分线。这种方法也可以在古埃及找到(Karpinski，1915: 2)。

另一方面，吉尔伽美什的史诗，众所周知大约产生于公元前2000年，在九个例子中包括象征力量的公牛的象征，而“天堂的公牛”，由Anu为Ishtar创造的干旱的化身，出现了两次(Sandars，1972: 87)。在巴比伦地区，有点凸起的椭圆形被称为靶心是很自然的。

总之，古巴比伦人区分了薄椭圆形和厚椭圆形。注意，在圆心O的外接矩形中(见图20)，点D构成等边三角形。等边三角形和小圆的交点决定了六边形的两条边。当然，它不是正六边形，但它接近99.9% (Allen，2013: 31)。

看着Naram-Sin(公元前2254-2218年)纪念碑的顶部(见图21(a))，美索不达米亚艺术的一种典型方法是使用两个太阳圆盘描绘战争场景，设计成8星多边形，中间有条纹矩形。设计成八星多边形的太阳圆盘在公元前三世纪末也很突出(见图21(b))。图21(b)显示了南美索不达米亚地区的独特风格，发现于苏萨。

图21：(A)Naram-Sin纪念碑顶部(b)在卢浮宫博物馆苏萨发现的纪念碑

此外，在IM 51979中，古巴比伦人展示了一个带有对角线的八角形(见图22，左)(Friberg, 2007a: 164)。对于IM 51979, 8星多边形意味着由3产生的Z8的子群就是Z8本身。穿过中心的四条线表示因子组Z8 / 4Z8。由于gcd(3,8)=1，古巴比伦数学一次绘制所有对角线。特别地，因为数字8是偶数，所以有一条对角线穿过原点。

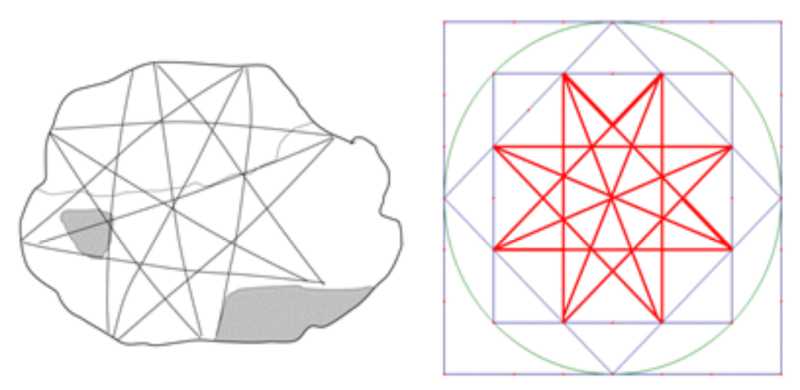
图22：古巴比伦8星多边形

在卡西王朝(Kassite Dynasty)的Meli-Shipak(公元前1186-1172年统治)时期，也发现了一个8点多边形。在kassiite Kudurru(图23)中，Meli-Shipak将她的女儿介绍给Shamash。星星象形文字从左到右象征着金星(伊什塔)、月亮(辛)和太阳(沙玛什)。

图23：梅利-希帕克国王(公元前1186-1172年统治)的库杜鲁，卢浮宫博物馆

在古巴比伦时期，8角星被包围在一个圆盘内(Black & Green，2014: 170)。在弓箭手的中楣上(大约公元前510年)，我们可以在伊师塔的八星多边形中找到圆形(见图24)。

图24：弓箭手中楣，大流士一世(约公元前510年)，卢浮宫博物馆

作为参考，让我们看看古埃及使用的八角形的例子。阿摩斯纸莎草纸的问题48是关于确定一个半径为9的圆的面积。文字是由Ahmose在Apophis统治的第三十三年写的(刘升，1979: 84，伯纳尔，2002: 328)。这本书的背面有一个注解(刘升，1979: 119)。它指的是在一个不知名的法老统治的第11年“Set和Isis的诞生”。有不确定性，但是Bernal (2002: 328)提出公元前1628年是基于Thera火山爆发的Apophis的第11年。根据他的学说，我们声称阿赫默斯大约在公元前1606年写了这本书。

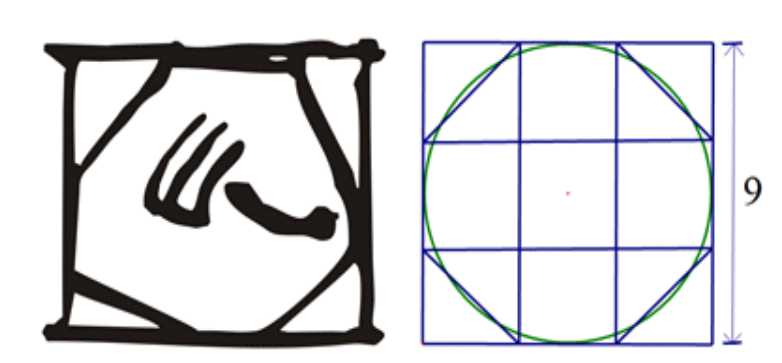
图25：Ahmose对48题的绘图和Vogel的猜想

根据Vogel的主张，伪八边形的面积是63(图25，右)。对应一个边长为√63的正方形，大约√64 = 8。因此，圆的面积公式(82可能起源于其中d是圆的直径(Gillings，1975: 142-3)。结果，古巴比伦人用矩形和八边形找到了圆的面积(参见Diop，1981: 243)。

在公元前1400年左右使用的纸莎草盒子(见图26)(卢浮宫博物馆指南)中，我们可以看到4星、8星和16星的多边形，这看起来很复杂，但却是基于八角形的结构。盖子可以通过固定一个点来旋转(卢浮宫博物馆指南)。观察图26中星形多边形的设计，我们可以看到，至少在公元前15世纪，埃及人在他们的设计中使用了8点多边形。

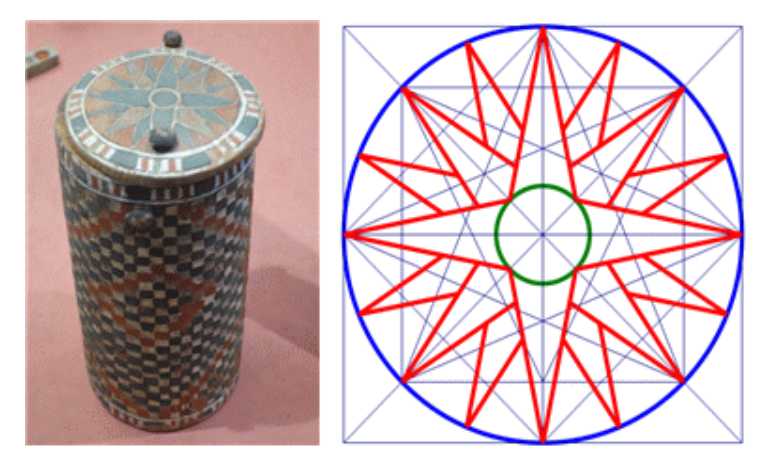
图26：埃及的纸莎草盒及其星形多边形设计，卢浮宫博物馆

菲莱神庙圆柱的横截面是一个8重的玫瑰花结(Diop，1981: 298)，在拉美西斯三世统治时期(公元前1184-1153)，8重和10重的玫瑰花结被用作宫殿装饰品。特别是，巴比伦人发现了一个凹方形的区域(Katz，2009: 16)，它用于装饰8重玫瑰花结(图27，左)。

图27：宫殿装饰和圆柱横截面模型，卢浮宫博物馆

结论

八角形在整个穆斯林世界广泛使用的原因是由于文化的相互关系、自然环境以及数学家和工匠之间的合作。我们从以下四个方面陈述了原因:

1.前伊斯兰土著女神的象征成功了。

伊南娜/伊师塔，爱与战争的女神，是苏美尔文化中的高级神(坎贝尔，2013: 79)。大约在公元前4000年，乌鲁克在两个神庙区域的统治地位是显而易见的：后来的库尔拉瓦神殿和早期的伊南娜管区，后者后来包含了伊南娜神殿。其他的苏美尔城市有向伊南娜提供祭品的习俗(斯卡雷和法甘，1997: 73-4)。在第四个千年，定义伊南娜的角色和功能的最重要的文献是瓦尔卡花瓶(柯林斯，1994: 113)。我们可以在Jemdet Nasr时期(Wolkstein & Kramer，1983: 184)的一枚圆柱印章上找到两颗伊南娜的8角星。在古巴比伦时期，金星通常是伊南娜/伊师塔的象征，八角星被包围在一个圆盘内(黑色和绿色，2014: 170)。请看下面图28中显示的伊南娜之星。

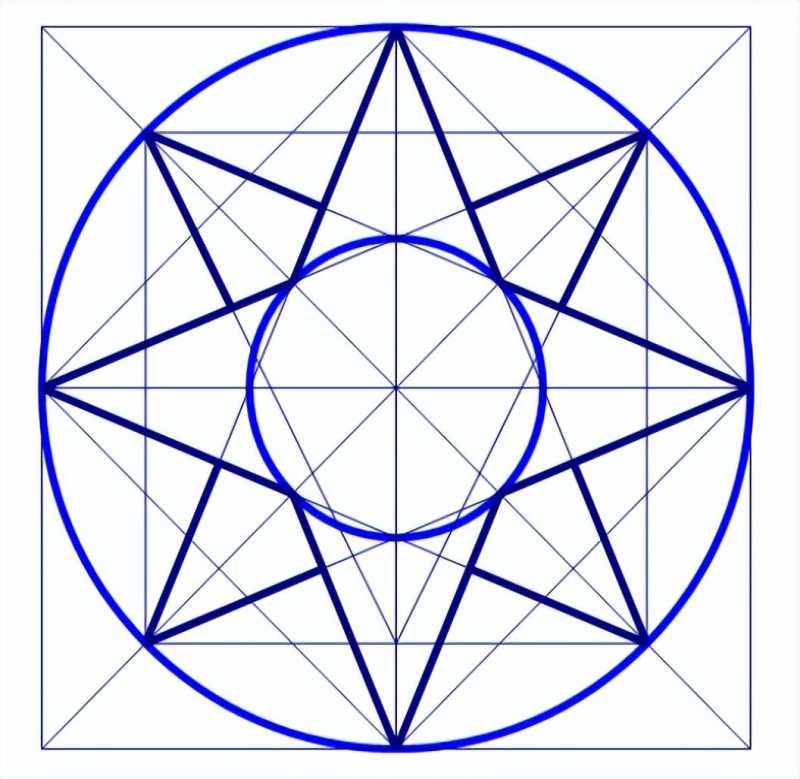
图28：伊南娜之星的建造

在新亚述时期，8重玫瑰花结偶尔取代星星作为伊南娜的象征(黑与绿，2014:156-7)。在库杜鲁，一颗8点星通常放在新月旁边，这是象征着月亮的神罪。

2. 建筑师和艺术家使用正多边形来解决艺术冲突。

在9世纪末，几何主题被穆斯林建筑师和艺术家采用。假设规则多边形在满足他们的艺术冲突中发挥了作用。在公共(或宗教)艺术中，几何作品经常与植物、书法以及无肖像的风景结合使用，因此，正多边形似乎有助于在伊斯兰地区单调的环境和城市景观中建立装饰氛围(Lewis, 2002: 96)。

3.《古兰经》中提到了8:

(《古兰经》69章17节)“众天使将站在山的两侧，到那日，有八个人在他们以上担当你的重任。”

这个段落可以被看作是一种心理因素，很容易适应伊斯兰艺术的常规八角形形式。

多年来，许多学者对《古兰经》进行了评论，但没有提到数字8。然而，它可以被解释为接受八角形的重要贡献，八角形在穆罕默德之前就广泛存在于美索不达米亚和埃及。

4.艺术家和数学家定期举行会议，在伊斯兰艺术设计方面取得了很大进展。

数学家如Abulwafa(10世纪)、Omar Khayyam(11世纪)、Al-Kashi(15世纪)和Efendi(16世纪末- 17世纪初)分别在巴格达、伊斯法罕、撒马尔罕和伊斯坦布尔与艺术家会面(Özdural 2000;171 - 172)。例如，Omar Khayyam解了一个与特殊直角三角形有关的三次方程，其中斜边等于短边和斜边的垂线之和。Omar Khayyam认为

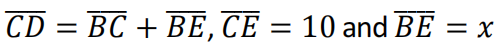
（图29左）

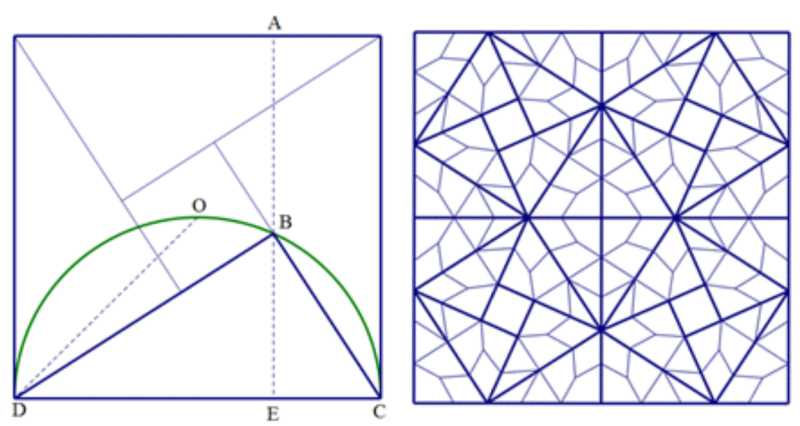
图29：欧玛尔·海亚姆的三角T尺和波斯手稿169

因此，他将会议上提出的问题简化为用圆和双曲线的交点求x3 + 200x=20x2 + 2000的解(Özudural, 1995: 58,59)。作为Omar Khayyam的术语，它是“一个立方和根等于平方和数字”，他还用t尺证明了如果AB= BC，那么CD= BC + BE (Özudural, 1995: 59,63)(图29，左)

参考文献

Abdullahi, Y. & Embi, M. (2013). Evolution of Islamic geometric patterns, Frontiers of Architectural Research 2, 243-251.

Allen, J. (2013). Drawing geometry; Fourth edition, Edinburgh: Floris Books.

Bernal, M. (2002). Black Athena, Vol II; Fifth edition, New Jersey: Rutgers University Press.

Black, J. & Green, A. (2014). Gods, demons and symbols of ancient Mesopotamia; Eighth Edition, Texas: University of Texas Press.

Campbell, J. (2013). Goddess; First Edition, California: New World Library.

Chace, A. (1979). The Rhind mathematical papyrus; Photo-offset Edition, Virginia: NCTM.

Chorbachi, W. (1989). In the tower of babel: Beyond symmetry in Islamic design, Computers Math. Applic 17(4-6), 751-789.

Collins, P. (1994). The Sumerian goddess Inanna (3400-2200 B.C.), Institute of Archaeology 5, 103-118.

Critchlow, K. (1999). Islamic patterns; U.S. Edition, Vermont: Inner Traditions.

Cromwell, P. & Beltrami, E. (2011). The whirling kites of Isfahan: Geometric variations on a theme, The Mathematical Intelligence 33(3), 84-93.

Diop, C. A. (1981). Civilization or barbarism: An authentic anthropology; translation by Y. M. Ngemi, First Edition, Illinois: Lawrence Hill Books.

Dummit, D.& Foote, R. (2004). Abstract algebra; Third Edition, New Jersey: John Wiley & Sons.

El-Said, I. & Parman, A. (1976). Geometric concepts in Islamic art; First Edition, London: World of Islam Festival Publishing Company.

Friberg, J. (2005). Unexpected links between Egyptian and Babylonian mathematics; First Edition, Singapore: World Scientific Publishing Company.

Friberg, J. (2007a). Amazing traces of a Babylonian origin in Greek Mathematics; First Edition, Singapore: World Scientific Publishing Company.

Friberg, J. (2007b). A remarkable collection of Babylonian mathematical texts; First Edition, New Nork: Springer.

Gillings, R. (1975). Mathematics in the time of the pharaohs; Second Edition, Massachusetts: MIT Press.

Huber, P. (1955). Zu einem mathematischen Keilschrifttext (VAT 8512), Isis 46(2), 104-106.

Katz, V. (2009). A history of mathematics; Third Edition, New York: Addison-Wesley.

Karpinski, L. (1915). Robert of Chester’s Latin translation of the algebra of Al-Khowarizmi, First Edition, London: The MacMillian Company.

Lewis, B. (ed.). (2002). The world of Islam; Second Edition, New York: Thames & Hudson.

Makovicky, E. (1986). Symmetrology of art: Coloured and generalized symmetries, Comp. & Maths. With Appls. 12B, 949-980.

Martin, G. (1982). Transformation geometry; First Edition, New York: Springer.

Necipoğlu, G. (1995). The Topkapi scroll-Geometry and ornament in Islamic architecture; First Edition, Santa Monica: Getty Center.

Neugebauer, O. (1957). The exact sciences in antiquity; Second Edition, New York: Dover.

Ossendrijver, M. (2016). Ancient Babylonian astronomers calculated Jupiter’s position from the area under a timevelocity graph, Science 351(6272), 482-484.

Özdural, A. (1995). Mathematicians, and “Conversazioni” with artisans, J. of the Soc. of Architectural Historians 54(1), 54-71.

Özdural, A. (2000). Mathematics and art: Connections between theory and practice in the medieval Islamic world, Historia Mathematica 27, 171-201.

Park, J. & Kim, S. (2017). Islamic art designs: Focused on the Uzbekistan ceramic penal and sidewalk block designs, J. Korean Association of Islamic Studies 27(2), 31-60.

Robson, E. (2008). Mathematics in ancient Iraq; First Edition, New Jersey: Princeton Univ. Press.

Sandas, N. (1972). The epic of Gilgamesh; Third Edition, New York: Penguin Books.

Scarre, C.& Fagan, B. (1997). Ancient civilizations; Third Edition, New Jersey: Pearson.

The Holy Quran, Chapter 69, verse 17 (69:17)

Wolkstein, D. & Kramer, S. (1983). Inanna: Queen of heaven and earth; First Edition, New York: Harper & Row.

Jeanam Park, Cultural and Mathematical Meanings of Regular Octagons in Mesopotamia: Examining Islamic Art Designs

青山不改，绿水长流，在下告退。

转发随意，转载请联系张大少本尊。